Theorie zu den Würfel-Aufgaben

1) Mit welcher Wahrscheinlichkeit kann ich mit einem Würfel eine 6 würfeln?

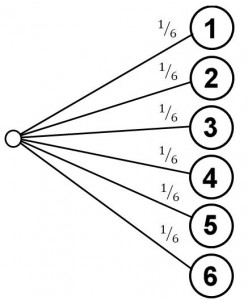
Der normale Würfel hat 6 Flächen. Auf jede dieser Flächen fällt er mit der gleichen Wahrscheinlichkeit. Wenn wir ihn werfen, muss er auf eine der 6 Flächen fallen, jede Fläche kommt mit der Wahrscheinlichkeit von 1/6 nach oben.

w = Anzahl günstige Fälle / Anzahl mögliche Fälle = 1/6 = 0.1667 = 16.67%

Aufgabe 2: Mit welcher Wahrscheinlichkeit würfle ich mit 2 Würfeln zwei 6-er?

Möglich sind die folgenden Würfelkombinationen:

1 1            2 1            3 1            4 1            5 1            6 1
1 2            2 2            3 2            4 2            5 2            6 2
1 3            2 3            3 3            4 3            5 3            6 3
1 4            2 4            3 4            4 4            5 4            6 4
1 5            2 5            3 5            4 5            5 5            6 5
1 6            2 6            3 6            4 6            5 6            6 6

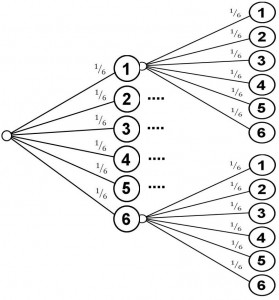
Günstig ist nur ein Fall (6; 6), möglich sind aber 36 Fälle

w = 1 / 36 = 1 / (6*6) = 0.02777 = 2.78%

Aufgaben zu den Wahrscheinlichkeiten mit Würfeln

Aufgabe 1

Zum Würfeln wird ein Tetraeder benutzt, der auf seinen vier Seiten mit 1, 2, 3 und 4 beschriftet ist. Als Ergebnis zählt diejenige Augenzahl, die auf der Grundfläche steht. Der Tetraeder wird fünfmal hintereinander geworfen. Wie viele verschiedene mögliche Ergebnisse gibt es, wenn
a) keine weiteren Bedingungen vorliegen,
b) fünfmal dieselbe Augenzahl auftreten soll,
c) die erste und die letzte Augenzahl übereinstimmen sollen,
d) die Augenzahl 1 genau einmal auftreten soll,
e) die Augenzahl 1 mindestens einmal auftreten soll,
f) die Augenzahl 1 genau zweimal auftreten soll,
g) die Augenzahl 1 höchstens zweimal auftreten soll ?

Lösungen Aufgabe 1

a) alle möglichen Ereignisse sind 4⁵ = 1024. Also 1024 Ereignisse.

b) fünfmal dieselbe Augenzahl wäre 11111 oder 22222 oder 33333 oder 44444. Das sind 4 Ereignisse. Als Rechnung: 1⁵ · 4 = 4

c) Wenn die erste und die letzte Augenzahl gleich sein sollen, reduzieren sich die Ereignisse. Wurf 2 bis 4, also die drei mittleren Würfe, umfassen alle möglichen Ereignisse, also 4³ = 64. Jedes dieser Ereignisse erweitert sich durch die Bedingung gleiche Augenzahl am Anfang und am Schluss um den Faktor 4. Also sind es 64 · 4 = 256.

d) 1 soll genau einmal auftreten. Somit wird jede Kombination mit 1 beginnen.

Aufgabe 2

Chevalier de Mére-Aufgabe, dargestellt und gelöst hier.

Aufgabe 3

 

 

Welches ist der beste Würfel?

Statistische Untersuchung von Spielwürfeln

In einem kleinen Versuch wollen wir herausfinden, wie „gut“ ein Würfel ist. Unter einem „guten“ Würfel verstehe ich ein Würfel, der jede Augenzahl mit der gleichen Wahrscheinlichkeit zeigt.

Wir suchen aus Gesellschaftsspielen ein paar verschiedene Würfel heraus.

Wir würfeln mit allen verschiedenen Würfeln getrennt (oder ein paar Personen würfeln mit je einem Würfel). Mit einem Würfelbecher wird das Resultat besser. Das Ergebnis eines jeden Wurfes wird in eine Protokolltabelle eingetragen.

Darunter tragen wir die (sogenannten absoluten) Häufigkeiten für die einzelnen Augenzahlen ein. Wir vergleichen die verschiedenen Würfel. Gib es Unterschiede? Unter die absoluten Häufigkeiten tragen wir die relativen Häufigkeiten ein.

Erster Würfel

	1	2	3	4	5	6
Strichliste	IIIII IIIII IIIII II	IIIII IIIII II	IIIII IIIII IIIII IIII	IIIII IIIII IIIII I	IIIII IIIII IIIII IIIII I	IIIII IIIII IIIII III
absolute Häufigkeit	17	12	19	16	21	18	103
relative Häufigkeit	0.165	0.1165	0.1845	0.1553	0.2039	0.1748

Die relative Häufigkeit einer Augenzahl gibt die Wahrscheinlichkeit an dieser Stichprobe für diese Augenzahl.

Gibt es nun einen Test, den ich anwenden kann, um zu entscheiden, ob ich den Würfel als einen guten Würfel bezeichnen kann?

• Allgemeine Einführung in die Wahrscheinlichkeitslehre
• Wahrscheinlichkeit mit Würfeln
• Schweine-Würfel: Spiel, Theorie, Lösungen
• Chevalier de Mere
• Kombinatorik