Die Vigenère-Verschlüsselung ist eine Weiterentwicklung der Caesar-Verschlüsselung. Blaise de Vigenère hatte als Diplomat oft mit geheimen Botschaften zu tun. Seine Beschäftigung mit der Kryptographie führte zur Entwicklung einer wirklich starken Verschlüsselungsmethode, die heute als Vigenère-Verschlüsselung oder Chiffre bekannt geworden ist.
Blaise de Vigenère (1523 – 1596)

Nachdem er den Staatsdienst verlassen hatte, widmete er sich nur noch dem Schreiben von Büchern und der Wissenschaft der Verschlüsselung, der Kryptographie.

TRAICTÉ DES CHIFFRES OU SECRETES MANIERES D’ESSAI
Vigenère schrieb mehr als 20 Bücher. Am bekanntesten ist das Traicté des chiffres, ou secrete maniere d’escrire. Darin beschreibt er seine Verschlüsselungsmethode, die fast 300 Jahre nicht geknackt werden konnte.
De Vigenère hat Ideen von Johannes Trithemius (1462–1516), Giovan Battista Bellaso (ca. 1505–1568/81), Leon Battista Alberti (1404–1472) und vor allem Giovanni Battista della Porta (1535–1615) aufgegriffen und zu seiner Verschlüsselungsmethode kombiniert.
Erst Charles Babbage zeigte um 1850 eine systematische Methode, wie man Vigenère-Verschlüsselungen entziffern (dechiffrieren) konnte. Aber auch im 1. Weltkrieg wurde diese Verschlüsselungsmethode noch angewendet.
Vigenère – die Weiterentwicklung der Caesar-Verschlüsselung
Die Verschlüsselung nach Vigenère ist eine Entwicklung, die die simple Verschiebung der Buchstaben, wie in der Caesar-Verschlüsselung, erweitert aber trotzdem für das Chiffrieren und das Dechiffrieren praktikabel ist.
Bei der Caesar-Verschlüsselung kann durch die simple Verschiebung der einzelnen Buchstaben um einen festen Wert ein chiffrierter Text innerhalb kurzer Zeit dechiffriert werden. Sie ist durch die Buchstabenhäufigkeit leicht zu knacken.
Bei der Vigenère Verschlüsselung ist die Buchstaben-Verschiebung nicht gleichbleibend, wie bei der Caesar-Verschlüsselung. Sie wird mittels eines Code-Worts oder Schlüsselwort vorgenommen. Dieses Code-Wort darf natürlich nur dem Empfänger bekannt sein.
Als Code-Wort wird ein beliebig langer Schlüssel gewählt. In diesem Beispiel ist es MEINSTEIN. Alle Zeichen des Schlüssels (Code-Wortes) müssen demselben Alphabet angehören wie die Zeichen des zu verschlüsselnden Klartextes. Zur Demonstration seien dies wieder die Grossbuchstaben A bis Z.
Als Beispiel wird nun der Satz „WIR SCHREIBEN GEHEIM“ mit dem Schlüssel „MEINSTEIN“ verschlüsselt.
Als Erstes wird das Schlüsselwort Buchstabe für Buchstabe unter den Klartext gesetzt und so oft wiederholt, bis er der Länge des Klartextes entspricht.
WIRSCHREIBENGEHEIM (Klartext)
MEINSTEINMEINSTEIN (Schlüssel)
Folgendes zur Hilfe: Wir setzen zu jedem Buchstaben den Zahlenwert des Alphabets. Um diesen Wert sollen die Buchstaben verschoben werden:
| A | 0 | G | 6 | M | 12 | S | 18 | Y | 24 | ||||
| B | 1 | H | 7 | N | 13 | T | 19 | Z | 25 | ||||
| C | 2 | I | 8 | O | 14 | U | 20 | ||||||
| D | 3 | J | 9 | P | 15 | V | 21 | ||||||
| E | 4 | K | 10 | Q | 16 | W | 22 | ||||||
| F | 5 | L | 11 | R | 17 | X | 23 |
Nun wird für jeden Buchstaben separat die Caesar-Verschlüsselung angewendet, für jeden Buchstaben mit dem jeweiligen Schlüsselwort-Buchstaben. Dies gibt jedem Buchstaben des Klartextes einen anderen Verschiebungswert.
Als Hilfe und auch für Berechnungen können wir unter den Klartext und den Schlüssel die Buchstabenzahl (siehe obige Tabelle) hinschreiben.
Das sieht dann so aus:
| Klartext | W | I | R | S | C | H | R | E | I | B | E | N | G | E | H | E | I | M |
| x | 22 | 8 | 17 | 18 | 2 | 7 | 17 | 4 | 8 | 1 | 4 | 13 | 6 | 4 | 7 | 4 | 8 | 12 |
| Schlüssel | M | E | I | N | S | T | E | I | N | M | E | I | N | S | T | E | I | N |
| y | 12 | 4 | 8 | 13 | 18 | 19 | 4 | 8 | 13 | 12 | 4 | 8 | 13 | 18 | 19 | 4 | 8 | 13 |
| (x+y) mod 26 | 8 | 12 | 25 | 6 | 20 | 0 | 21 | 12 | 21 | 13 | 8 | 21 | 19 | 22 | 0 | 8 | 16 | 25 |
| Geheimtext | I | M | Z | F | U | A | V | M | V | N | I | V | T | W | A | I | Q | Z |
Daraus entsteht aus dem Klartext mit dem Schlüsselwort der Geheimtext. Infos zur Modulo-Rechnung findest du hier.
|
Klartext |
WIRSCHREIBENGEHEIM MEINSTEIN IMZFUAVMVNIVTWAIQZ |
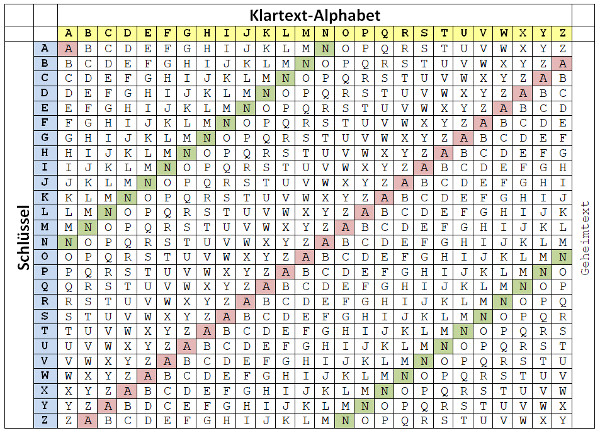
Die Verschlüsselung mit Hilfe des Vigenère-Quadrats
Mit der sogenannten Tabula recta, einer quadratischen Tabelle aller 26 x 26 Buchstaben, später als carré de Vigenère oder Vigenère-Quadrat bezeichnet, kann die Verschlüsselung einfach durchgeführt werden:
Vorgehen: Wir beginnen mit dem ersten Buchstaben (W) vom Klartext (gelbes Alphabet waagrecht). Von diesem geht es senkrecht hinunter bis zum ersten Buchstaben vom Schlüssel (M) (blaues Alphabet senkrecht).
In der Tabelle kann nun der erste verschlüsselte Buchstabe (I) abgelesen werden. Dasselbe für den zweiten und dritten Buchstaben (3.).
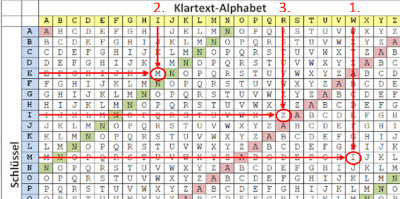
Hier ein Bild vom Vigenère-Quadrat. Eine Vorlage kann hier heruntergeladen werden.
Warum die Vigenère-Chiffre lange als unknackbar galt
Die Vigenère-Chiffre ist – im Gegensatz zur Caesar-Verschlüsselung – eine polyalphabetische Verschlüsselung. Jeder Buchstabe wird mit einem neuen Alphabet-Schlüssel chiffriert.
Während bei der Caesar-Chiffre mit Brute Force nur 26 Verschiebungen ausprobiert werden müssen, um den Geheimtext zu dechiffrieren, müssen bei der Vigenère-Chiffre viel mehr Schlüssel ausprobiert werden. Je länger das Code-Wort (Schlüssel-Wort), desto grösser werden die Möglichkeiten:
Aufwand für eine Brute Force-Attacke
| Schlüssellänge 1 Schlüssellänge 2 Schlüssellänge 3 Schlüssellänge 4 Schlüssellänge 5 Schlüssellänge n |
= = = = = = |
26 Möglichkeiten 262 = 263 = 264 = 265 = 26n |
26 Möglichkeiten (Caesar-Chiffre) 676 Möglichkeiten 17’576 Möglichkeiten 456’976 Möglichkeiten 11’881’376 Möglichkeiten Möglichkeiten |
Wenn die Schlüsseltextlänge 5 Zeichen umfasst (n = 5), gibt es bereits 26 + 262 + 263 + 264 + 265 = 12’356’630 Möglichkeiten. Bei einer Schlüssellänge von 100 Zeichen ergibt sich bereits eine unvorstellbar grosse Zahl von Möglichkeiten (Zahl mit über 140 Stellen).
Heute gibt es – vor allem auch mit Hilfe von Computer-Geschwindigkeit – Möglichkeiten, das Schlüsselwort und somit auch die Vigenère-Chiffre zu entschlüsseln.
Dechiffrieren von Vigenère
Hier geht’s zum Dechiffrieren eines mit Vigenère verschlüsselten Textes