Rechteck und Quadrat

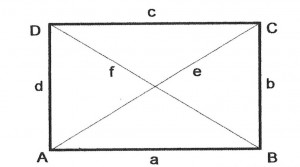
Das Rechteck

Alle vier Winkel sind rechtwinklig.
Die gegenüberliegenden Seiten sind gleich lang: a = c und b = d
Die Diagonalen e und f halbieren sich und sind beide gleich lang: e = f

Umfang:
u = a + b + c + d
u = 2a + 2b

Fläche:
A = a ⋅ b

Diagonale:
e = √ (a2 + b2)

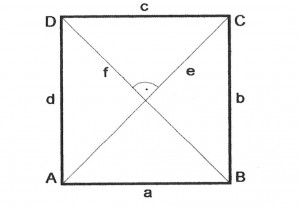
Das Quadrat

Alle vier Seiten sind gleich lang: a = b = c = d
Vier rechte Winkel.
Die Diagonalen e und f sind gleich lang und halbieren sich (in einem rechten Winkel).

Umfang:
u = a + b + c + d = 4a

Fläche:
A = a2

Diagonale:
e = a ⋅ √ (2)

Berechnungen des Rechtecks

Aufgabe	1	2	3	4	5	6	7
Länge a	20 cm	15 m		16 cm
Breite b	4 cm		22 mm
Fläche A		45 m²	6 mm²		40 m²	12 cm²
Umfang u				50 cm	26 m		100 m
Diagonale e						5 cm	40 m

Die Berechnungen der Aufgaben aus der Tabelle werden nun alle durchgeführt:

Beispiel 1: Gegeben die beiden Seiten a und b des Rechtecks

Gegeben:
a = 20cm
b = 4cm
Gesucht sind A, u, e
Gesetze
A = a · b = 80cm²
u = 2a + 2b = 48cm
e = √ (a² + b²) = 20.40cm

Beispiel 2: Gegeben die Seite a und die Fläche A des Rechtecks

Gegeben sind:
a = 15m
A = 45 m²
Gesucht werden b, u, e (Diagonale)
Gesetze dafür:
A = a · b → b = A/a = 3m
u = 2a + 2b = 36m
e = √ (a² + b²) = 15.30m

Beispiel 3: Gegeben die Seite b und die Fläche A des Rechtecks

Gegeben sind:
b = 22mm
A = 6mm²
Gesucht sind: a, u, e
Gesetze dafür:
A = a · b → a = A/b = 0.272727 mm²
u = 2a + 2b = 44.4545 mm
e = √ (a² + b²) = 22.00169 mm

Beispiel 4: Gegeben a und Umfang u

Gegeben sind: a = 16cm und u = 50cm
Mit der Umfangsformel u = 2a + 2b können wir b ermitteln
2b = u – 2a
b = 1/2 · (u – 2a) = 1/2 · (50 – 2·16) = 1/2 · 18 = 9cm
Fläche A = a · b = 144cm²
Diagonale e = √ (a² + b²) = 18.3576 cm

Beispiel 5: Gegeben sind A und u

Gegeben sind
A = 40m2
u = 26m
Gesucht sind: a, b, e
Gesetze
u/2 = a + b = 13m
40m2 = a · b
a = 13 – b
40 = (13 – b) · b
b² – 13b + 40 = 0
mit der Mitternachtsformel ergeben sich die beiden Lösungen:
b₁ = 8, b₂ = 5
wenn b = 8m ist, dann ist a = 5m
wenn a = 4m ist, dann ist b = 8m
e = √ (a² + b²) = 9.43m

Beispiel 6: Gegeben ist Fläche A und Diagonale e

Gegeben
A = 12cm²
e = 5cm
Gesucht sind: a, b, u
Gesetze

Beispiel 7: Gegeben

Gegeben
u = 100m
e = 40m
Gesucht sind: a, b, A
Gesetze

Berechnungen des Quadrates

Aufgabe	1	2	3	4
Quadratseite a	40cm
Quadratfläche A		100m²
Umfang u			60mm
Diagonale e				200cm

Beispiel 1: Gegeben Quadratseite a

Geg: a = 40cm
Ges: A, u, e (Diagonale)
Ge:
A = a · a = 1600cm2
u = 4a = 160cm
e = 56.58 cm

Beispiel 2: Gegeben Fläche A

Geg: A = 100m²

Beispiel 3: Gegeben Umfang u