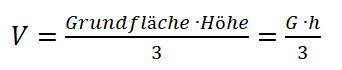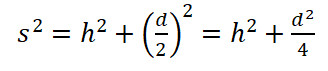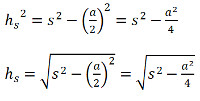Pyramiden kennen wir aus dem Geschichtsunterricht über die Alten Ägypter. Die grösste griechische Pyramide, die Cheops-Pyramide zeigt die wahre Pracht der Pyramidenform.
Mathematik der quadratischen Pyramiden
Spitze Körper – Pyramide und Kegel – entstehen aus den Körpern Würfel, Quader, Prismen oder Zylinder. Die Berechnung von Volumen ist immer gleich: Grundfläche mal Höhe durch drei.
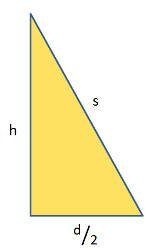
Bei der Berechnung der Oberfläche braucht man neben der Grundfläche den sogenannten Mantel. Für die Berechnungen der spitzen Körper ist der Pythagoras nötig, den muss man sich zuerst erarbeiten. Weiter ist es wichtig, dass man sich ein räumliches Vorstellungsvermögen aneignet.
Pyramiden (eckige spitze Körper)
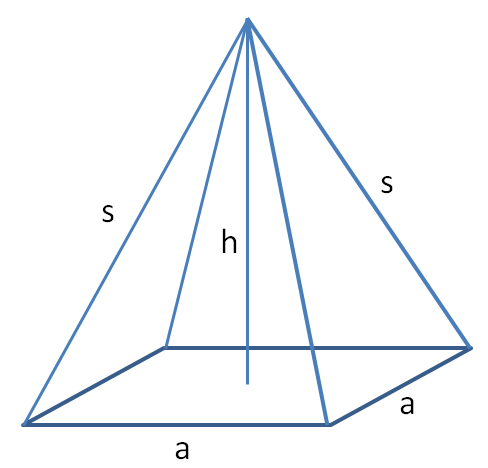
Pyramiden haben eine Grundfläche, die aus einem Dreieck, Viereck oder Vieleck besteht. Von jeder Ecke der Grundfläche führt eine Seitenkante s zur gemeinsamen Spitze.
Die quadratische Pyramide
Die quadratische Pyramide ist am einfachsten zu berechnen.
Aufgaben und Übungen
Berechnung einer quadratischen Pyramide
Gegeben:
Quadratseite a = 5cm
Pyramidenhöhe h = 8cm
Gesucht:
Grundfläche G
Volumen V
Seitenhöhe hs
Mantel M
Oberfläche O
Gesetze:
G = a ⋅ a = 25 cm2
V = G ⋅ h : 3 = 67 cm3
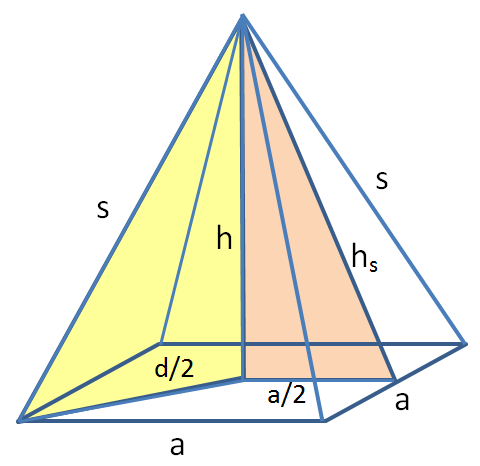
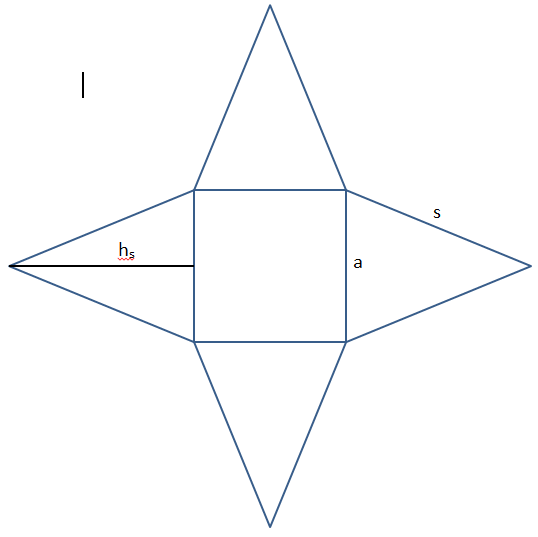
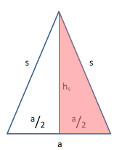
Der Mantel zu berechnen ist etwas aufwändiger als das Volumen. Der Mantel besteht aus 4 gleichschenkligen Dreiecken, deren Grundlinie die Quadratseite ist.
hs = wurzel (h2 + (a/2)2 ) = 8.38 cm
Dreiecksfläche A = (a ⋅ hs / 2) = 20.95 cm2
Mantel M = 4 ⋅ A = 83.82 cm2
Oberfläche O = M + G = 108 cm2