Mit der Caesar-Verschlüsselung geheime Texte schreiben
Eine der bekanntesten, sehr einfachen und deshalb auch unsicheren Methoden der Verschlüsselung ist die Caesar-Verschlüsselung (Cesar-Chiffrierung). Ihren Namen hat sie vom römischen Caesar, der so geheime Botschaften versendete.
Beispiel
Aus dem Original-Satz (Klartext) werden durch eine Caesar-Verschlüsselung die Buchstaben jedes Wortes im Alphabet verschoben. Im folgenden Beispiel um 9 (k = 9)
In der Abbildung oben (Verschlüsselungsschablone) sind die ersten drei Buchstaben eingerahmt.
| Klartext Verschlüsselt |
Franz jagt im komplett verwahrlosten Taxi quer durch Bayern Oajwi sjpc rv txvyuncc enafjqauxbcnw Cjgr zdna mdalq Kjhnaw |
Drehschablone zum Chiffrieren und Dechiffrieren
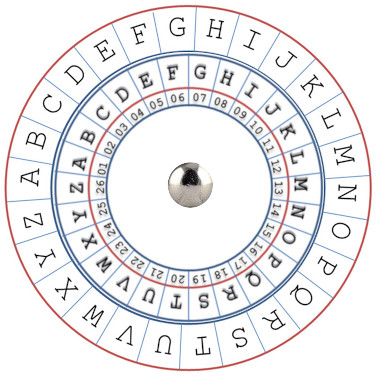
Mit der folgenden Drehschablone kann einfach chiffriert bzw. dechiffriert werden. Sie lässt sich einfach herstellen und ist eine gute praktische Arbeit für eine Lektion.
Hier kann eine Vorlage zum Basteln kostenlos heruntergeladen werden.
Methoden der Dechiffrierung (Entschlüsselung)
Doppelbuchstaben bleiben Doppelbuchstaben. Häufige Zeichen in der deutschen Sprache sind e und n. Indem man alle Verschiebungen im Alphabet durchspielt, findet man mit Fleiss (oder mit Hilfe eines Computerprogramms) den Text heraus.
Entschlüsseln durch Ausprobieren
Hier ein kurzer Geheimtext, der mit der Caesar-Verschlüsselung chiffriert ist. Wir kennen aber die Verschiebungszahl nicht.
HIV QIRWGL MWX IVWX AMVOPMGL XSX AIRR RMIQERH QILV ER MLR HIROX
Eine Dechiffrierung dieses Textes fällt einfach. Ich schreibe den Satz 26 Mal auf, jede Zeile verschiebe ich die Buchstaben um eine Stelle. Damit wird eine Zeile lesbar: Es ist die 23. Zeile. Damit ist k = 4.
1 HIV QIRWGL MWX IVWX AMVOPMGL XSX AIRR RMIQERH QILV ER MLR HIROX
2 IJW RJSXHM NXY JWXY BNWPQNHM YTY BJSS SNJRFSI RJMW FS NMS IJSPY
3 JKX SKTYIN OYZ KXYZ COXQROIN ZUZ CKTT TOKSGTJ SKNX GT ONT JKTQZ
4 KLY TLUZJO PZA LYZA DPYRSPJO AVA DLUU UPLTHUK TLOY HU POU KLURA
5 LMZ UMVAKP QAB MZAB EQZSTQKP BWB EMVV VQMUIVL UMPZ IV QPV LMVSB
6 MNA VNWBLQ RBC NABC FRATURLQ CXC FNWW WRNVJWM VNQA JW RQW MNWTC
7 NOB WOXCMR SCD OBCD GSBUVSMR DYD GOXX XSOWKXN WORB KX SRX NOXUD
8 OPC XPYDNS TDE PCDE HTCVWTNS EZE HPYY YTPXLYO XPSC LY TSY OPYVE
9 PQD YQZEOT UEF QDEF IUDWXUOT FAF IQZZ ZUQYMZP YQTD MZ UTZ PQZWF
10 QRE ZRAFPU VFG REFG JVEXYVPU GBG JRAA AVRZNAQ ZRUE NA VUA QRAXG
11 RSF ASBGQV WGH SFGH KWFYZWQV HCH KSBB BWSAOBR ASVF OB WVB RSBYH
12 STG BTCHRW XHI TGHI LXGZAXRW IDI LTCC CXTBPCS BTWG PC XWC STCZI
13 TUH CUDISX YIJ UHIJ MYHABYSX JEJ MUDD DYUCQDT CUXH QD YXD TUDAJ
14 UVI DVEJTY ZJK VIJK NZIBCZTY KFK NVEE EZVDREU DVYI RE ZYE UVEBK
15 VWJ EWFKUZ AKL WJKL OAJCDAUZ LGL OWFF FAWESFV EWZJ SF AZF VWFCL
16 WXK FXGLVA BLM XKLM PBKDEBVA MHM PXGG GBXFTGW FXAK TG BAG WXGDM
17 XYL GYHMWB CMN YLMN QCLEFCWB NIN QYHH HCYGUHX GYBL UH CBH XYHEN
18 YZM HZINXC DNO ZMNO RDMFGDXC OJO RZII IDZHVIY HZCM VI DCI YZIFO
19 ZAN IAJOYD EOP ANOP SENGHEYD PKP SAJJ JEAIWJZ IADN WJ EDJ ZAJGP
20 ABO JBKPZE FPQ BOPQ TFOHIFZE QLQ TBKK KFBJXKA JBEO XK FEK ABKHQ
21 BCP KCLQAF GQR CPQR UGPIJGAF RMR UCLL LGCKYLB KCFP YL GFL BCLIR
22 CDQ LDMRBG HRS DQRS VHQJKHBG SNS VDMM MHDLZMC LDGQ ZM HGM CDMJS
23 DER MENSCH IST ERST WIRKLICH TOT WENN NIEMAND MEHR AN IHN DENKT
24 EFS NFOTDI JTU FSTU XJSLMJDI UPU XFOO OJFNBOE NFIS BO JIO EFOLU
25 FGT OGPUEJ KUV GTUV YKTMNKEJ VQV YGPP PKGOCPF OGJT CP KJP FGPMV
26 GHU PHQVFK LVW HUVW ZLUNOLFK WRW ZHQQ QLHPDQG PHKU DQ LKQ GHQNW
Entschlüsselung durch Analyse
Das Vorgehen des Ausprobierens ist aber etwas mühsam. Vielleicht möchten wir etwas analytischer an die Entzifferung gehen.
Hier ein nächstes Beispiel:
MNAVXWMRBCJDOPNPJWPNWMRNPXUMWNWBCNAWUNRWYAJWPNWJVQRVVNUQNUUDWMTUJAMNAFJUMBCNQCBLQ FJAIDWMBLQFNRPNCDWMJDBMNWFRNBNWBCNRPNCMNAFNRBBNWNKNUFDWMNAKJAFRNRBCMRNFNUCBXBCRUU NDWMRWMNAMJNVVADWPQDNUUNBXCAJDURLQDWMBXQXUMJUBNRWNBCRUUNTJVVNAFXRQAMNBCJPNBSJVVNA ENABLQUJONWDWMENAPNBBNWBXUUCBNQCRQAMNWVXWMMXACBCNQNWNARBCWDAQJUKIDBNQNWDWMRBCMXLQ ADWMDWMBLQXNWBXBRWMFXQUVJWLQNBJLQNWMRNFRAPNCAXBCKNUJLQNWFNRUDWBANJDPNWBRNWRLQCBNQ WFRABCXUINVNWBLQNWTRWMNABRWMNRCNUJAVNBDNWMNADWMFRBBNWPJAWRLQCERNUFRABYRWWNWUDOCPN BYRWBCNDWMBDLQNWERNUNTDNWBCNDWMTXVVNWFNRCNAEXWMNVIRNUPXCCUJBBDWBMNRWQNRUBLQJDNWJD OWRLQCBENAPJNWPURLQBCAJDNWWRLQCNRCNUTNRCDWBOANDWUJBBDWBNRWOJNUCRPFNAMNWDWMEXAMRAQ RNAJDONAMNWFRNTRWMNAOAXVVDWMOAXNQURLQBNRWFXUUBCNWMURLQBXWMNAPAJNVNWJDBMRNBNAFNUCD WBWNQVNWMDALQNRWNWBJWOCNWCXMDWMFNWWMDDWBPNWXVVNWUJBBDWBRWQRVVNUTXVVNWMDDWBNAQNAAD WMDWBNAPXCCBXUNPCNDLQMNWWRQAKADNMNARWPXCCNBWJVNWWRNMNATJUCRBCMNAJKNWMQJDLQENABLQX WDWBPXCCVRCBCAJONWDWMUJBBDWBADQRPBLQUJONWDWMDWBNAWTAJWTNWWJLQKJAJDLQ
Buchstabenhäufigkeit
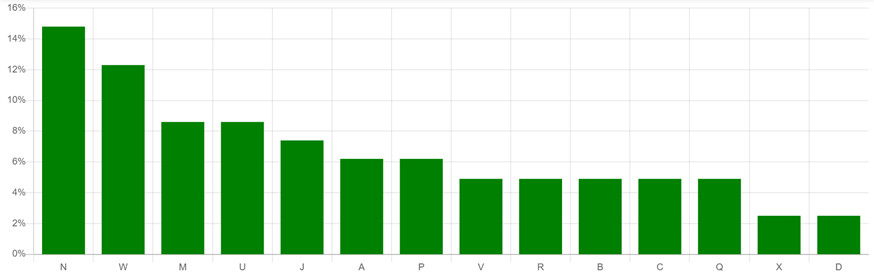
Die Buchstaben kommen in jeder Sprache in einer recht konstanten Häufigkeit vor. Wir vergleichen die relative Häufigkeit der Buchstaben mit der relativen Häufigkeit der Buchstaben im Text.
| Häufigkeit der Buchstaben in der deutschen Sprache |
Häufigkeit der Buchstaben im verschlüsselten Text |
| E 17.48% N 9.84% I 7.73% R 7.54% S 6.83%. |
N 15.12% W 12.20% B 8.45% R 6.78% A 6.47% |
MeAVXnMRBCJDOPePJWPeWMRePXUMWeWBCeAWUeRWYAJWPeWJVQRVVeUQeUUDWMTUJAMNAFJUMBCNQCBLQ