Die Möndchen des Hippokrates sind eine klassische Mathe-Aufgabe. Hier wird bewiesen, dass die gelben Möndchen zusammen die selbe Fläche haben wie das rechtwinklige Dreieck.
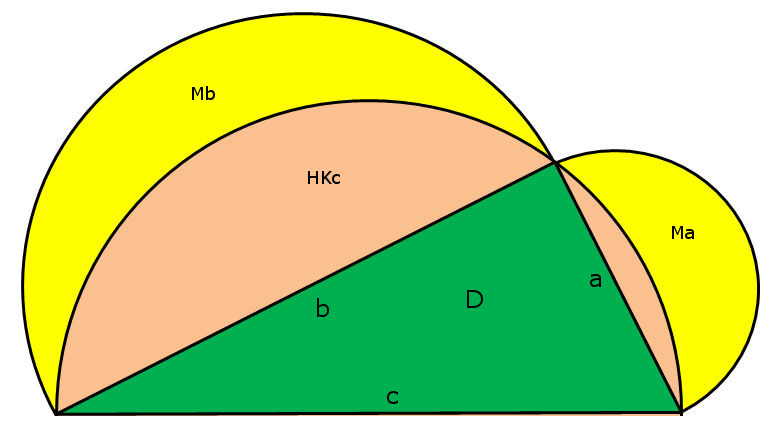
Gegeben: Seitenlängen des rechtwinkligen Dreiecks a, b, c
wobei c2 = a2 + b2 (das Dreieck ist rechtwinklig, was wir bereits am Thales-Kreis erkennen können). Es gilt also der Pythagoras.
Flächenberechnung der Möndchen
Idee: Grünes Dreieck plus Halbkreis über b plus Halbkreis über a minus Halbkreis über c.
Möndchen M = ½ ⋅ a ⋅ b + ½ ⋅ (b/2)2 ⋅ π + ½ ⋅ (a/2)2 ⋅ π – ½ (c/2)2 ⋅ π
wir vereinfachen den Ausdruck, indem wir ½ ⋅ π ausklammern:
Möndchen M = ½ ⋅ a ⋅ b + ½ ⋅ π (a ⋅ b + (b/2)2 + (a/2)2 – (c/2)2)
nach dem Pythagoras ist b2 + a2 – c2 = 0, somit ist auch (b/2)2 + (a/2)2 – (c/2)2) = 0
also ist die Fläche der Möndchen M = ½ ⋅ a ⋅ b , was der Fläche des Dreiecks entspricht.
q.e.d. (quot erat demonstrandum, was zu beweisen war)