Wir leben in einer Welt voller Winkel, wo Winkel und Bogenmass überall vorkommen. Bei Häusern treffen wir meistens den rechten Winkel an, so bei senkrechten Wänden auf waagrechten Boden. Auch in den Himmelsrichtungen stecken Winkelwerte. nach rechts abbiegen heisst insofern: in einem Winkelwert von 90° nach rechts fahren.
Definition Winkel in der Geometrie
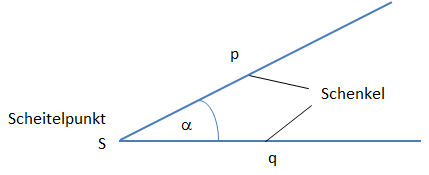
Zwei Strahlen p und q, die von einem Punkt (Scheitelpunkt S) ausgehen, bilden einen WinkeI α. Die beiden Strahlen sind die Scheitel des Winkels α.
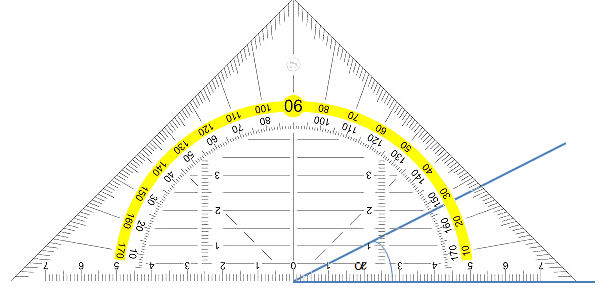
Wir können Winkelwerte mit dem Geodreieck herausfinden: Auf der Skala (gelb) können wir hier 27° ablesen. Gerade darunter sind die Winkelwerte in umgekehrter Reihenfolge sehen.
Spezialwinkel
Wir kennen verschiedene Spezialwinkel:
- Vollwinkel: 360°, WinkeI eines ganzen Kreises.
- Gestreckter_Winkel: 180°, die beiden Schenkel sind waagrecht gestreckt.
- Nullwinkel: 0°, die beiden Schenkel liegen aufeinander.
- Rechter_Winkel: 90°, der Viertel eines Vollwinkels
- Spitzer Winkel: WinkeI kleiner als 90°
- Stumpfer Winkel: WinkeI grösser als 90° und kleiner als 180°
- Überstumpfer Winke: WinkeI zwischen 180° und 360°
Winkelmasse
Das Gradmass
Das Gradmass erhalten wir, indem wir einen Kreis mit Radien in 360 deckungsgleiche Teile (Kreisausschnitte) zerlegen.
Das Gradmass kann weiter unterteilt werden:
1° = 60 ‚ (Minuten)
1‘ = 60 “ (Sekunden)
1° = 60 ‚ = 3600 “
Das Bogenmass
Das Bogenmass misst den WinkeI durch den Bogen über dem WinkeI im Einheitskreis. Der Vollwinkel hat einen Kreisbogen von 2π. Ein gestreckter WinkeI entspricht π.
Allgemein: b = (α / 180°) ⋅ π
360° = 2π
180° = π
90° = π/2
60° = π/3
45° = π/4
Konstruktion von Winkeln (mit Zirkel und Lineal)
| Rechter Winkel (90°) | Wir errichten das Lot auf einen Punkt (Scheitel) einer Geraden und erhalten den rechten W. |
| 60° – Winkel | Konstruktion eines gleichseitigen Dreiecks. Alle Winkel betragen 60°. Wir zeichnen eine Gerade und tragen mit dem Zirkel eine Strecke ab. Von beiden Punkten auf der Gerade ziehen wir Kreisbogen. Es entsteht über und unter der Geraden ein gleichseitiges Dreieck. |
| 45° W. | Wir halbieren den 90° – Winkel. |
| 22.5° W. | Wir halbieren den 45° – Winkel |
| 11.25° | Wir halbieren den 22.5° – Winkel. |
| 30° | Halbieren des 60° – Winkels |
| 15° | Halbieren des 30° – Winkels |
| 120° | Verdoppeln von 60° – Winkels |
| 150° | Wir addieren einen 90° und einen 60° – WinkeI |
| etc. |