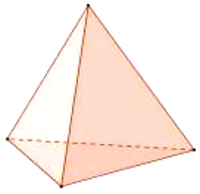
 Wir betrachten das Tetraeder
Wir betrachten das Tetraeder
Das Tetraeder besteht aus vier gleichseitigen Dreiecken, vier Ecken und sechs gleich langen Kanten der Länge a.
Das Wort Tetraeder kommt aus dem Griechischen: tetra heisst vier und hédra heisst Flächen, also das Tetraeder ist ein Vierflächner oder ein Vierflach.
Tetraeder gehören sowohl zu den spitzen Körpern, wie auch zu den platonischen Körpern.
Was hat Tetrapack mit Tetraedern zu tun?
Man muss schon ein gewisses Alter haben, um zu wissen, dass die Verpackungsfirma Tetra Pack früher ihre Milch in Tetraeder-Form verkauft hat.



Berechnung der Oberfläche des Tetraeders
Die Oberfläche ist relativ einfach zu berechnen. Wir bestimmen den Flächeninhalt von einem gleichseitigen Dreieck und multiplizieren diesen mit 4.
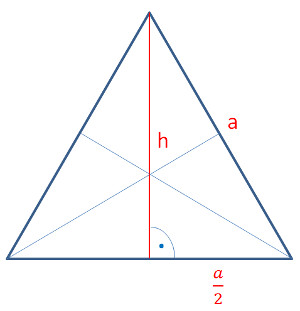
Das gleichseitige Dreieck wird symmetrisch halbiert. So entsteht ein rechtwinkliges Dreieck. Mit ihm kann die Flächenhöhe h berechnet werden:

Damit ist die Dreiecksfläche A:
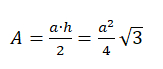
Berechnung des Tetraeder-Volumens
Das Volumen eines spitzen Körpers wird hier erklärt. Hier erfährst du, warum man bei spitzen Körpern das Volumen immer durch drei teilen muss.

Die Grundfläche ist das gleichseitige Dreieck, das wir oben berechnet haben. Die Körperhöhe H ist nun aber nicht die Flächenhöhe h, sondern die Körperhöhe H. Über sie wollen wir uns einige Gedanken machen.
Die Höhe des Tetraeders
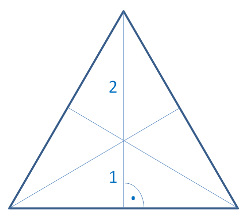
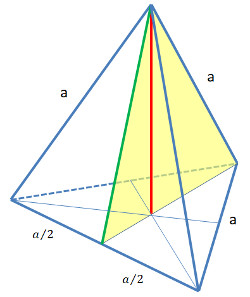
Die Körperhöhe steht auf dem Mittelpunkt des gleichseitigen Dreiecks. Den Mittelpunkt finden wir über die Seitenhalbierenden. Diese schneiden sich im Verhältnis 2 : 1.
Die rot gezeichnete Körperhöhe berechnen wir wieder mit dem Pythagoras:
Kathete 1: 2/3 der Flächenhöhe
Kathete 2: Körperhöhe
Hypothenuse: Kante a
Das ergibt:
(Kathete 2)2 = Hypothenuse2 – (Kathete 1)2
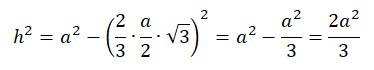
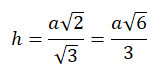
Die Volumenformel des Tetraeders

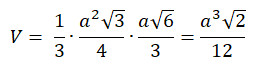
Ansichten
Versuche mit der gegebenen Vorlage einen Tetraeder zu basteln und durch Drehung die hier gezeigten Ansichten zu finden.
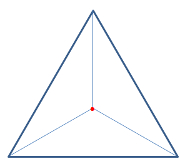 Spitze zeigt gegen dich |
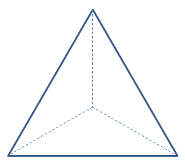 Spizte zeigt von dir weg |
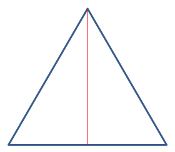 Kante gegen dich |
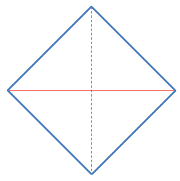 Kante horizontal |
 Ecken rechts unten aufeinander |
Tetraeder selber basteln
Hier kannst du eine Vorlage zum Basteln eines Tetraeders und ausdrucken.
Tetraeder um uns herum
Beton Tetrapoden brechen die Wellen an der Küste. Rechts ein Bild, wie diese Tetrapoden in Formen gegossen werden.


Links