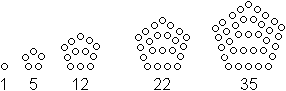
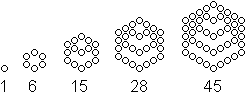Was ist eine Zahlenfolge?
Eine Zahlenfolge ist eine Funktion (f). Man ordnet einer Zahl, die Element der natürlichen Zahlen (N) ist, einem Wert aus den reellen Zahlen (R) zu. Die natürliche Zahl, der man einem Wert zuordnet, heisst n (Nummer, vergleichbar mit dem x-Wert bei anderen Funktionen, man fängt in aller Regel mit 1 an und nicht mit 0). Der Wert (n-tes Folgeglied) heisst an. Das heisst, statt a1, a2, a3 usw. zu schreiben, fasst man es kurz zu an zusammen.
Die einfachste aller Zahlenfolgen ist die Zahlenfolgen der natürlichen Zahlen:
Dargestellt werden kann sie mit folgender Abbildung:
1, 2, 3, 4, 5, …… n
Die Folge beginnt mit 1.
Das Bildungsgesetz ist ganz einfach: von Glied zu Glied kommt eins dazu.
Das allgemeine Glied heisst: an = n
Figurierte Zahlen: Eine figurierte Zahl (oder Figurenzahl) ist eine natürliche Zahl, die man durch eine Figur (mit Elementen, Kugeln, Platten etc) darstellen kann.
Die Zahlenfolge der geraden Zahlen kann mit folgendem Muster dargestellt werden:
2, 4, 6, 8, ….
Das Bildungsgesetz lautet: füge immer 2 Werte dazu.
Das allgemeine Glied: an = 2n
Die Zahlenfolge der ungeraden Zahlen könnte folgendes Muster haben:
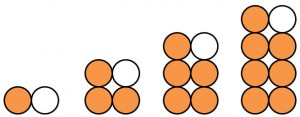
1, 3, 5, 7, …..
Das Bildungsgesetz lautet: Beginne mit 2. Ziehe einen Wert ab. Füge weitere 2 dazu und ziehe eins ab.
Allgemeines Glied: an = 2n-1
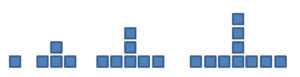
Weitere Muster
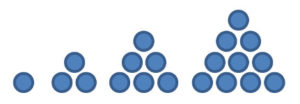
Dreieckszahlen
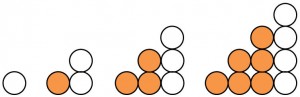
Die Folge der Dreieckszahlen lautet:
1, 3, 6, 10, 15, …..
1, 1+2, 1+2+3, 1+2+3+4, …..
Das allgemeine Glied dieser Zahlenfolge kann man mit der Formel: n * (n + 1) / 2 bestimmen.
Erklärung: Will ich z.B. wissen, wie gross das 10. Glied dieser Folge heisst, so weiss ich, dass es mühsam berechnet werden könnte mit:
1+2+3+4+5+6+7+8+9+10
Trick: Ich addiere das erste und das letzte, das zweite und das zweitletzte … das letzte und das erste. Das ist dann genau doppelt so viel wie die Lösung!
1 + 10 = 11
2 + 9 = 11
3 + 8 = 11
4 + 7 = 11
5 + 6 = 11
6 + 5 = 11
7 + 4 = 11
8 + 3 = 11
9 + 2 = 11
10 + 1 = 11
Addiert sind es 10 * 11, was aber genau das Doppelte der Lösung ist! Also ist die Lösung:
a10 = 10 * 11 / 2
Allgemein (mit dem allgemeinen Glied n)
| 1 | 2 | 3 | … | n – 2 | n – 1 | n |
| n | n – 1 | n – 2 | … | 3 | 2 | 1 |
| n + 1 | n + 1 | n + 1 | n + 1 | n + 1 | n + 1 | n + 1 |
Ich summiere alle n der n+1 und erhalte n ( n + 1) (was aber genau das Doppelte der Lösung ist).
an = n * (n + 1) / 2
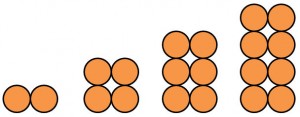
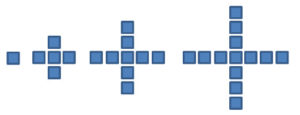
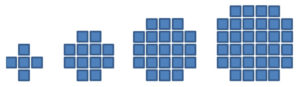
Viereckszahlen
Bereits die Zahlenfolge der geraden Zahlen gehören eigentlich zu den Viereckszahlen. Hier aber eine nächste Musterabfolge figurierter Zahlen:
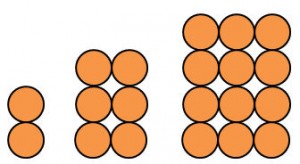
Die dazugehörigen Zahlen sind:
2, 6, 12, ….
Um die nächste Zahl zu finden, müssen wir das Bildungsgesetz herausfinden:
Das erste Muster ist: 1*2 (für n=1)
Das zweite Muster ist 2*3 (für n=2)
Das dritte Muster ist 3*4 (für n=3)
Also lautet die Formel für das n-te Glied:
an = n ( n + 1)
Quadratzahlen sind auch Viereckszahlen:
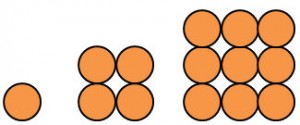
Die Zahlenfolge lautet:
1, 4, 9, 16, 25, …..
Das Bildungsgesetz ist einfach, die Berechnung eines n-ten Gliedes auch:
an = n2
Weitere Musterfolgen
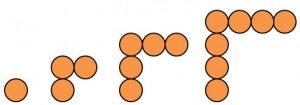
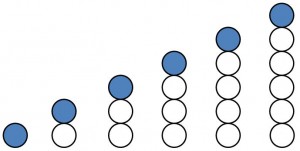
Folge: 1, 3, 5, 7
Bildungsgesetz: in jeder neuen Figur kommen zwei Kugeln dazu.
Allgemeines Glied: an = 2n – 1
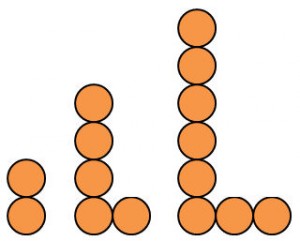
Folge: 2, 5, 8, ….
Bildungsgesetz: In jeder Figur kommen 3 Kugeln dazu.
Allgemeines Glied: an = 3n – 1
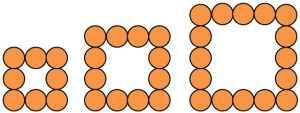
Folge: 8, 12, 16, …
Bildungsgesetz: In jeder neuen Figur kommen 4 neue Kugeln dazu.
Allgemeines Glied: an = 4n + 4
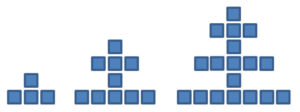
Fünfeckszahlen
Sechseckzahlen
Weitere Folgen durch figurierte Zahlen







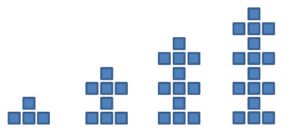

![]()




Links
www.mathematische-basteleien.de/figuriertezahlen.htm