Diagonale mit dem Pythagoras berechnen
Flächendiagonalen
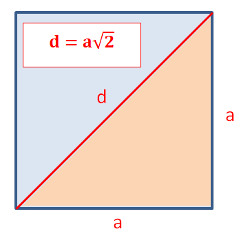
Die Diagonale eines Quadrates ist mit dem Pythagoras einfach zu berechnen:
Erklärung
Gemäss dem Pythagoras ist
d2 = a2 + a2
d2 = 2a2
die Wurzel draus ergibt:
d = a √2
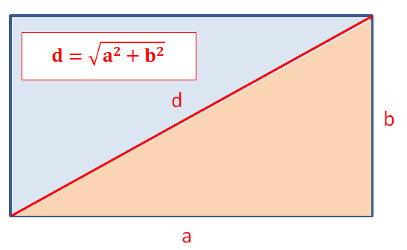
Auch die Diagonale eines Rechtecks lässt sich mit dem Pythagoras leicht berechnen:
Erklärung
Gemäss dem Pythagoras ist
d2 = a2 + b2
die Wurzel draus ergibt:
d = √ (a2 + b2 )
Raumdiagonalen
Raumdiagonalen sind eigentlich ebenso einfach zu berechnen, doch muss man sich den Raum vorstellen können.
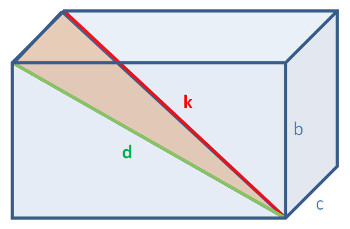
Die Raumdiagonale in einem Quader
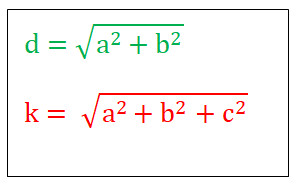
Erklärung:
Mit der Flächendiagonale d aus wird ein rechtwinkliges Dreieck dck gezeichnet und erneut der Pythagoras angewendet. Daraus ergibt sich die obige Formel.
Die Raumdiagonale in einem Würfel
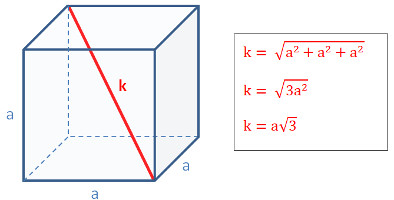
Erklärung:
Wie beim Quader nur hier viel einfacher: alle Seiten sind a, damit haben wir die einfache Formel k2 = 3a2
Die Wurzel lässt sich aus a2 ziehen und Wurzel 3 bleibt bestehen. Also a mal Wurzel 3.