An Beispielen zeige ich dir, wie man Bruchgleichungen löst.

Bei dieser Gleichung stören vorerst nur die Brüche. Diese müssen durch Erweitern entfernt werden.
Wir erweitern die Brüche mit dem Hauptnenner: 5*4*3
4*3(3z – 19) = 5*3(35 – z) + 4*5(2z – 25)
12(3z – 19) = 15(35 – z) + 20(2z – 25)
36z – 221 = 525 – 15z + 40z – 500
36z + 15z – 40z = 500 + 525 + 221
11z = 1246
z = 113

Etwas schwieriger wird es, wenn die Variable im Nenner ist:

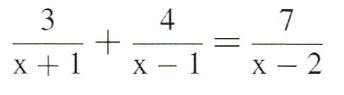
Hauptnenner: (x+1)(x-1)(x-2)
(x-1)(x-2)3 + (x+1)(x-2)4 = (x+1)(x-1)7
(x2 – 2x -x + 2)3 + (x2 – 2x +x -2)4 = (x2 – x + x – 1)7
(x2 – 3x + 2)3 + (x2 – x – 2)4 = (x2 – 1)7
3×2 – 9x + 6 + 4×2 – 4x – 8 = 7×2 – 7
7×2 – 13x -2 = 7×2 – 7
– 13x – 2 = – 7
13x = 5
x = 5/13  (mit x≠-1, x≠1, x≠2)