Bi-nom bedeutet „zwei Namen“, Binome sind mathematische Ausdrücke, die zwei Variablen enthalten. Binomische Formeln sind Gesetze, die für Ausdrücke gelten  wie (a + b). Binomische Formeln erleichtern uns in der Mathematik, gewisse Aufgaben zu lösen.

Bevor du mit dem Thema loslegen kannst, solltest du jedoch die Grundlagen der Klammerrechnung beherrschen. Wenn du das hast, kannst du starten.

Erste Binomische Formel

(a + b)² = a² + 2ab + b²

Zweite Binomische Formel

(a – b)² = a² – 2ab + b²

Dritte Binomische Formel

(a + b)(a – b) = a² – b²

 

a und b können durch eine Zahl oder einen Term ersetzt werden

Für a und b können Zahlen oder ganze Terme eingesetzt werden. Aber die binomischen Formeln gelten immer noch gleich.

Für a = 3 und b = 7 lautet die erste binomische Formel:
(3 + 7)(3 + 7) = 9 + 2 · 3 · 7 + 49 = 100

Für a = c und b = 5 lautet die zweite binomische Formel:
(c – 5)(c – 5) = c² – 2 · 5c + 25

Für a = 2r und b = 4p lautet die dritte binomische Formel:
(2r + 4p)(2r – 4p) = 4r² – 16p²

 

Grafische Darstellung der binomischen Formel

Erste Binomische Formel: (a + b) · (a + b)

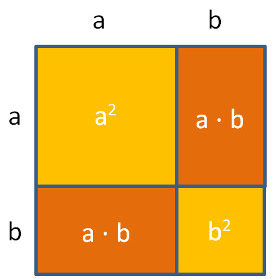
Wenn die senkrechte Quadratseite (a + b) mit der waagrechten Quadratseite (a + b) multipliziert wird, dann setzt sich die resultierende Fläche zusammen aus:

– dem grossen a²
– den beiden Rechtecken a · b
– und dem kleinen Quadrat b²

Also: (a + b) · (a + b) = a² + 2ab + b²

 

 

Zweite Binomische Formel: (a – b) · (a – b)

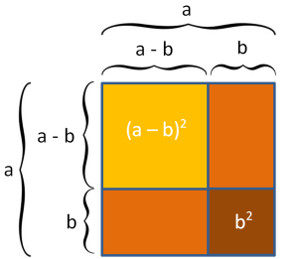
Die Formel a² – 2ab + b²  wird auch hier grafisch sichtbar, wenn auch nicht auf den ersten Blick:

Vom ganzen Quadrat (Seitenlänge a) wird zwei Mal ein Rechteck (a · b) abgezogen. Damit aber ist das braune, kleine Quadrat (b²) doppelt abgezogen und muss am Schluss einmal wieder dazugefügt werden. Es bleibt das gelbe Quadrat (a – b)² zurück.

Also: (a – b) (a – b) = a² – 2ab + b²

 

Dritte Binomische Formel: (a + b)(a – b)

Wir können die dritte Binomische Formel auf zwei verschiedene Arten erklären.

Erste Erklärungsvariante

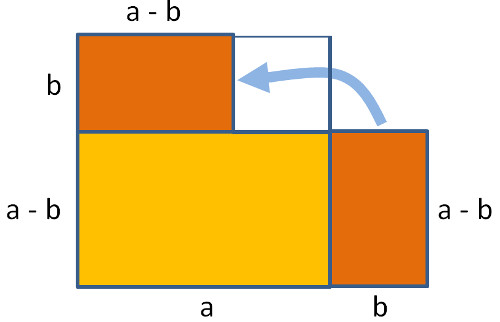
(a + b)(a – b) beschreibt das Rechteck unten bestehend aus dem gelben Teil und dem braunen Teil.

Wenn wir das braune Rechteck auf das gelbe schieben, sehen wir, dass dann gerade ein Quadrat (b²) fehlt (weisses Quadrat).

Deswegen ist (a + b)(a – b) auch das Quadrat über a minus das weisse Quadrat (b²), also a² – b².

 

Zweite Erklärungsvariante

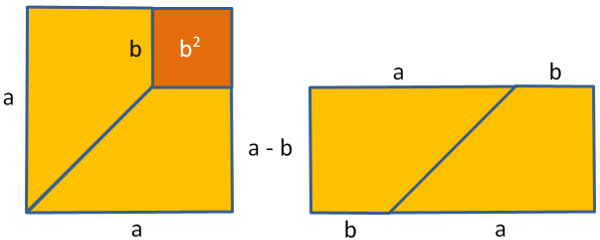
Das gelbe Rechteck rechts zeigt die Fläche von (a + b)(a – b).

Ordnet man die Trapez-Flächen anders, entsteht das linke Quadrat, bei dem grad das Quadrat von b fehlt (braune Fläche).

 

Übungen mit Lösungen

 

Faktorisieren von Trinomen

Hier siehst du, wie man Trinome faktorisiert.