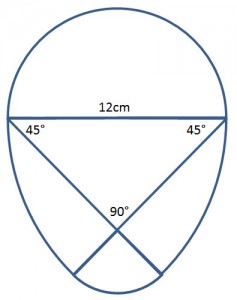
Löse hier die ultimative Ostereier-Aufgabe! Berechne die Fläche dieses Eies.

Gegeben

Durchmesser des oberen Halbkreises d = 12cm
Gleichschenkliges rechtwinkliges Dreieck mit c = 12cm

Überlegungen zur Figur

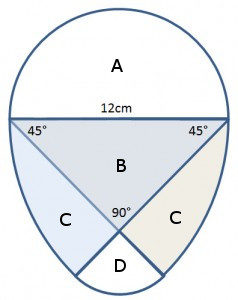Der obere Halbkreis (Fläche A) ist leicht zu erkennen. Sein Durchmesser beträgt 12cm.
Beim unteren Teil wird es schon etwas kniffliger… aber wir können es lösen!
Der mittlere Teil besteht besteht aus zwei übereinander gelegten Kreisausschnitten (Fläche B + C). Mit 45° handelt es sich um zwei Achtel-Kreise mit dem Radius von 12cm.
Wenn wir von einem Achtel-Kreis genau die Fläche des rechtwinkligen gleichschenkligen Dreiecks subtrahieren, erhalten wir die Fläche C.
Der unterste Viertel-Kreis hat den Radius r = 12cm – Kathete des rechtwinkligen Dreiecks.

Berechnung der Fläche

Fläche Halbkreis oben A = 0.5 ⋅ 6cm² ⋅ π = 56.55cm²
Achtel-Kreisausschnitt A = 0.125 ⋅ 12cm² ⋅ π = 56.55cm²
Für das Dreieck gilt: c² = 2 ⋅ k² 
Kathetenlänge k = Wurzel (c² / 2) = Wurzel (144cm²/2) = 8.485cm
Fläche des Dreiecks A = 36cm²
Radius des unteren kleinen Kreises r = 12cm – 8.485cm = 3.51cm
Viertel-Kreis unten A = 0.25 ⋅ r² ⋅ π = 9.70cm²

Total: A = 143.35cm²   

Zur nächsten Aufgabe

Zurück zur Auswahl der Kreisflächenberechnungen