Berechne die blaue Fläche!
Überlegungen und Ideen
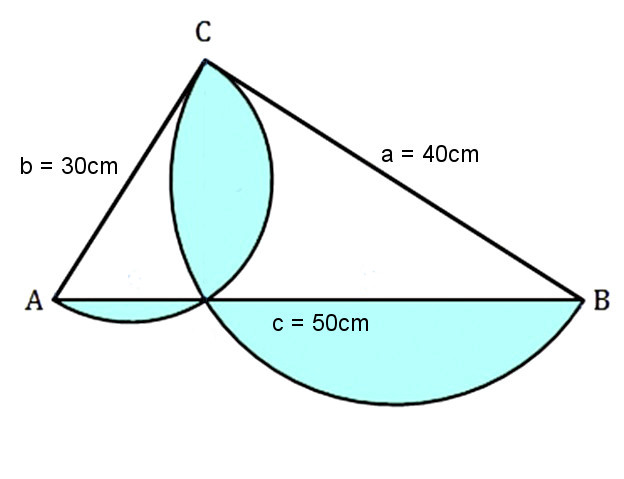
Das Dreieck ABC ist ein rechtwinkliges (wie sich einfach mit dem Pythagoras nachprüfen lässt). Zwei Halbkreise liegen über den Katheten a und b.
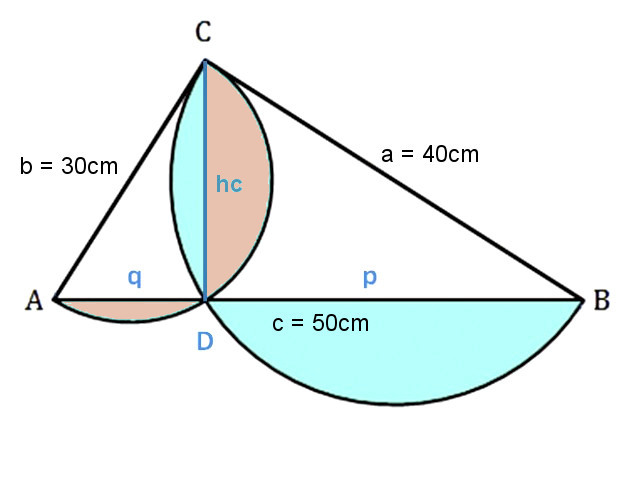
Ziehen wir die Höhe hc als Hilfslinie ein, so sehen wir, dass sich die Aufgabe leicht lösen lässt:
D teilt das Dreieck in zwei ebenfalls rechtwinklige Dreiecke: ADC und CDB.
Über die Seite a wird ein Halbkreis gezeichnet, ebenfalls über b.
Nun wird die Dreiecksfläche ABC vom ersten Halbkreis abgezogen und die Dreiecksfläche CDB vom zweiten Halbkreis.
Zurück bleiben die vier farbig gefüllten Kreisabschnitte, welche zusammen die blaue Fläche bilden.
Berechnung
Mit dem Kathetensatz des Euklid gelten folgende Zusammenhänge:
a2 = p ⋅ c
b2 = q ⋅ c
Damit ist:
p = a2 / c = 32cm
und
q = b2 / c = 18cm
Nach dem Höhensatz ist h2 = p ⋅ q , somit ist auch h bekannt: h = 24cm
Kreisabschnitte über der Seite a
Aa = Halbkreis über a minus Dreieck über a
Aa = 0.5 (20cm)2 ⋅ π – 0.5 ⋅ 32cm ⋅ 24cm = 244.32cm2
Kreisabschnitte über der Seite b
Ab = Halbkreis über b minus Dreieck über b
Ab = 0.5 (15cm)2 ⋅ π – 0.5 ⋅ 18cm ⋅ 24cm = 137.43cm2
Blaue Fläche zusammen
A = 381.75cm2