Emotionale Mathematik

Etwas für emotionale Mathematikstunden oder Mathe für Verliebte ;-)
Wir wollen wissen, wie gross die Herzfläche ist.

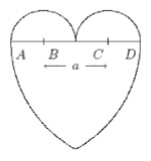
Untersuchung der Figur: Die beiden Halbkreise oben sind einfach zu berechnen. Zurück bleibt eine Schild-Form.

Sie wird gezeichnet mit dem Zirkel mit Radius 2a.

 

 

 

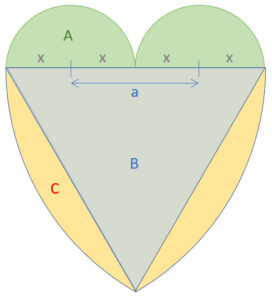
In den Schild kann ein gleichseitiges Dreieck gezeichnet werden. Dieses lässt sich berechnen, da wir eine Seite kennen (Seite = 2a).

Gleichzeitig versteckt sich hier eine 1/6 Kreisfläche mit dem Radius r = 2a. Sie schaut als C hervor und macht die Wölbung im unteren Teil des Herzens.

Idee: Um den Kreisabschnitt C zu berechnen subtrahieren wir vom 1/6 Kreis das gleichseitige Dreieck.

Berechnung

1. Berechnung der beiden kleinen Halbkreise (A)
2. Berechnung des 1/6 Kreises (B + C)
3. Berechnung des gleichseitigen Dreiecks B
4. Berechnung des Kreisabschnitts C
5. Zusammensetzen der ganzen Fläche (A + B + C + C)

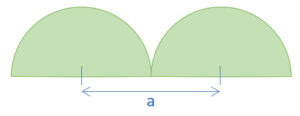
Erstens: Berechnung der kleinen Halbkreise (A)

Es sind zwei Halbkreise, daher können wir einen vollen Kreis berechnen.
Der Radius ist r = a/2.
Kreisformel: A = r2 ∙ π

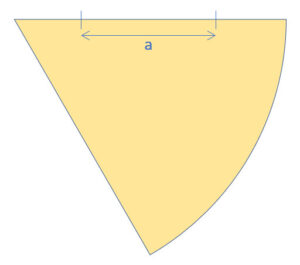
Zweitens: Berechnung des 1/6-Kreises (B + C)

Ein grosser Kreis mit dem Radius 2a muss durch 6 geteilt werden.
Der Radius ist r = 2a
Kreisformel: A = r2 ∙ π
Sechstel-Kreis: A/6 = (r2 ∙ π) : 6

Drittens: Berechnung des gleichseitigen Dreiecks (B)

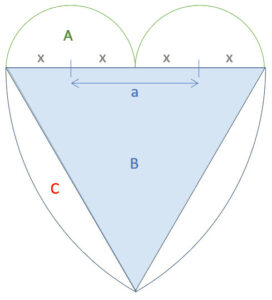
Siehe gleichseitiges Dreieck.

Viertens: Berechnung des Kreisabschnitts C

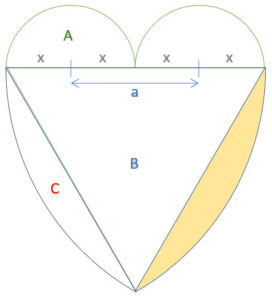
1/6-Kreis minus Dreieck B).

Fünftens: Alles zusammensetzen

A + B + C + C = A + B + 2C

Zur nächsten Aufgabe

Zurück zur Auswahl der Kreisflächenberechnungen