Jeder Gegenstand, jedes Material hat eine Dichte. Er kann schwer und klein sein wie viele Metallgegenstände, oder leicht und gross wie eine Styroporverpackung.

Also ist die Dichte eine relative Grösse. Relativ heisst, dass die Masse m pro Grösse (Volumen) ausgedrückt wird.

Die Fangfrage: Was ist schwerer, ein Kilo Federn oder ein Kilo Blei, bringt es auf den Punkt:
Beides ist natürlich gleich schwer, nur ist das Kilo Blei sehr viel kleiner als das Kilo Federn!
Genau genommen aber stimmt diese triviale Antwort nicht ganz: denn es müsste noch der Auftrieb berücksichtigt werden. Dieser ist grösser bei voluminösen Körpern wie Federn oder Styropor. Insofern stimmt die Antwort nur im Vakuum!
http://www.boojakascha.ch/indexXHTML.php?page=federVSblei
und als sokratischer „Wagenschein-Dialog“: (Text unten angefügt)

Definition der Dichte

Die Dichte ist definiert durch seine Masse und sein Volumen. Masse durch Volumen oder klarer:

Masse pro Volumen.

Je mehr Masse (kg) pro Volumen, desto dichter ist ein Material. Je mehr Kilogramm in ein festes Volumengefäss passen, desto grösser ist der Wert der Dichte.

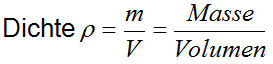
ρ (rho, kleines griechisches r) ist das Symbol für die Dichte
m ist die Masse
V ist das Volumen

Weil die Dichte die Masse pro Volumeneinheit ist, kann sie auch als relative Masse bezeichnet werden.

Die Masse ist überall im Universum gleich. Wenn wir aber das Gewicht pro Volumeneinheit nehmen, bezeichnet man das als Wichte, was nichts anderes ist als das relative Gewicht. Hier wird die Masse als Gewichtskraft angegeben, die z.B. anders ist auf der Erde als auf dem Mond.

Dichteanomalien

Normalerweise ziehen sich Stoffe bei zunehmender Kälte zusammen, werden kleiner und damit steigt ihre Dichte.

Beim Wasser ist das anders: Wasser ist am dichtesten bei 4°C. Darunter beginnen sich im Wasser bereits die ersten Kristalle zu bilden. Eis schwimmt, ist also leichter und voluminöser als Wasser. Dies kann auch beobachtet werden, wenn Wasser in einer Glasflasche gefriert und so diese zum Bersten bringt.

Dichteanomalien treten aber auch bei Antimon, Bismut, Gallium, Germanium, Plutonium, Silicium und Zirkoniumwolframat auf.

Wie wird die Dichte eines Körpers bestimmt?

Bei Gegenständen, deren Volumen einfach bestimmbar sind, wie zum Beispiel Quader, Würfel, Zusammengesetzte Körper, Zylinder und Kugel.

Beispiel Metallzylinder

Gegeben:
m = 602 g
d = 42mm = 4.2 cm
r = 21mm = 2.1 cm
h = 465.5mm = 5.45 cm

Gesucht: Dichte ρ

Gesetze:

V = r² · π · h = 75.51 cm³

ρ = m / V = 7.97 g/cm³

Wir finden, dass der Metallzylinder von der Dichte her aus legiertem Stahl bestehen könnte.

Beispiel Metallquader

Gegeben
l = 7.95 cm
b = 3 cm
h = 2.5 cm

Gesucht: Dichte

Gesetze:
V = l · b · h = 59.625 cm³
m = 159.2 g

ρ = m / V = 2.67 g/cm³

Es müsste sich also um Aluminium handeln (2.7 g/cm³).

Wenn das Volumen eines Körpers nicht leicht oder gar nicht bestimmt werden kann, müssen die Erkenntnisse von Archimedes angewendet werden:

      

Die Masse der Eisenerzkörner ist 30g

Verdrängt wurde 6.5cm³

Das Volumen ist also: V = 6.5 cm³

Damit ist die Dichte ρ = 30 / 6.5 = 4.6 g/cm³

Die Dichte dieser Körner ist also wesentlich grösser als die von anderen Steinen. Es handelt sich hier um ein Eisenerz.

 

Siehe auch: Archimedes und der Auftrieb

Die Dichte einiger Elemente und Stoffe

Stoff	Dichte in g/cm3
Luft	0.0013
Styropor	0.015
Kork	0.15
Fichtenholz	0.5
Benzin	0.75
Alkohol	0.79
Olivenholz	0.82 – 0.92
Eichenholz	0.9
Olivenöl	0.91
Eis	0.92
Wasser	1
PET	1.26
PVC	1.3
Sand	1.5
Kalkstein	1.55
Magnesium	1.74
Kies	2
Sandstein	2
Beton	2.1
Obsidian	2.33
Glas	2.5
Marmor	2.67
Aluminium	2.7
Granit	2.75
Zinn	7.29
Eisenstahl	7.7
Eisen	7.86
Stahl legiert	7.9
Messing	8.3
Kupfer	8.92
Silber	10.5
Blei	11.34
Quecksilber	13.55
Gold	19.32

Wasser hat die Dichte 1g/cm³ oder 1kg/dm³ oder 1 kg pro Liter.

Was schwerer ist als Wasser, also eine Dichte über 1 besitzt, sinkt im Wasser.
Was leichter ist als Wasser, also eine Dichte unter 1 besitzt, schwimmt im Wasser.
Alles mit einer Dichte um 1 herum, schwebt im Wasser.

Die Dichte des Wassers ist natürlich abhängig von Faktoren wie Temperatur, Druck und Reinheit (gelöste Stoffe im Wasser).

Einfache Aufgaben zur Dichte

Ergänze die Lücken

Masse in g	Volumen in cm3	Dichte in g/cm3	Stoff
150	55.55
450	9000
950		8.92
1500		19.32
	57.32	11.34
1200	1333.3
350		0.15
	1500	0.5
	62.73	13.55

Lösungen

Masse in g	Volumen in cm3	Dichte in g/cm3	Stoff
150	55.55	2.7	Aluminium
450	9000	0.05	Styropor
950	106.5	8.92	Kupfer
1500	77.64	19.32	Gold
650	57.32	11.34	Blei
1200	1333.3	0.9	Eiche
350	2333.33	0.15	Kork
750	1500	0.5	Fichte
850	62.73	13.55	Quecksilber

 

Weitere Aufgaben zur Dichte

Aufgaben (die Lösungen findest du darunter)

1. Welche Dichte (in g/cm³) hat ein Material, von dem der Würfel mit der Kantenlänge 17 mm die Masse 35,2g besitzt?
2. Welche Masse besitzen 0,53 Liter Dieselöl ρ = 0,86g/cm³)?
3. Welches Volumen hat ein Körper aus Aluminium (ρ = 2,7kg/dm³), dessen Masse 370g ist?
4. Die Tragfähigkeit eines Güterwagens der Bundesbahn sei 25t, seine Ladefläche 25m². Wie hoch darf Sand (ρ = 1,5g/cm³) in den Güterwagen eingefüllt werden?
   Hinweis: Es werde angenommen, dass die Ladung eine Quaderform hat.
5. Berechne die Dichte eines Körpers, der ein Volumen von 300 cm³ und eine Masse von 1200g besitzt.
6. Welches Volumen besitzt ein Körper aus Stahl mit einer Masse von einem Kilogramm? (Rho = 7.8 g/cm³)
7. Entscheide rechnerisch, ob du einen Würfel aus Styropor mit der Seitenlänge von 2 Meter hoch heben kannst. (Rho = 0.05 g/cm³). Hinweis: Rechne in g/cm³ um: kg/m³
8. Ein LKW darf maximal 20 t laden. Wie viele Stahltafeln mit den Abmessungen l = 4m, b = 1.5m, d = 8mm darf dieser LKW laden? (Rho = 7.8 g/cm³)

 

 

Lösungen: 1) r = 7.16g/cm³ 2) 0.4558g/cm³ 3) V = 0.137dm³ 4) h = 0.66cm 5) 4g/cm³, 6) V = 0.128dm³ 7) 400kg 8) 53 Tafeln

 

Allgemeine Aufgaben (mit Lösungen)

Aufgabe 1: Beantworte die Fragen

1a) Beschreibe – in Worten – was man unter Dichte versteht?

Dichte ist die Masse bezogen auf das Volumen, d.h. z.B. grosse Dichte ist schwer aber klein.

1b) Wie berechnet man die Dichte (Formel)?

ρ = m/V  Die Masse m wird mit der Waage bestimmt, das Volumen berechnet oder in einem Messbecher bestimmt. Das Volumen kann auch durch die Verdrängung von Wasser – wie es Archimedes gemacht hat – bestimmt werden. 

1c) Welche Dichte hat reines Wasser?

ρ = 1 kg/dm³  Die Dichte von Wasser ist 1. Was schwimmt, ist leichter als Wasser (ρ < 1), was sinkt, ist schwerer als Wasser (ρ > 1). 

Aufgabe 2: Berechne die Dichte

Zu einem Stoff sind folgende Informationen vorhanden. Masse: 5400g; Volumen: 2000cm³.

2a) Welche Dichte hat der Stoff?

ρ = 5400g/2000cm³ = 2.7g/cm³

2b) Um welchen Stoff könnte es sich handeln?

Aluminium

Aufgabe 3:

5 Liter Benzin haben eine Masse von 3.5kg. Wie gross ist die Dichte von Benzin?

ρ = 3.5kg / 5 Liter = 0.7 kg/dm³

Aufgabe 4:

4a) Löse die Formel der Dichte nach m auf.  m =

m = ρ * V

4b) Löse die Formel der Dichte nach V auf.  V =

V = m / ρ

 

Dialog aus der Seite: http://martin-wagenschein.de/Red/Schwere.htm

 

Was ist eigentlich schwerer, ein Kilogramm Blei oder ein Kilogramm Federn?

von Klaus Kohl

Wer kennt sie nicht, diese Scherzfrage?
Intuitiv will man sagen ‚das Blei‘ und weiß doch, dass es eine Scherzfrage ist, beides gleich schwer ist.
Man weiß es eben, aber stimmt es auch?

Am 3. Dezember 1996 wäre Martin Wagenschein 100 Jahre alt geworden, er starb vor acht Jahren. Ehrendoktor, mehrfacher Preisträger, wurde und wird er verehrt, interpretiert, missverstanden, beschimpft.
Jahrzehntelang hat er bis ins hohe Alter darum gekämpft, besonders den Mathematik- und Physikunterricht verständlicher zu gestalten, von Scheinwissen zu entrümpeln: „Verstehen des Verstehbaren ist ein Menschenrecht“ – „Verstehen lehren“ – „Rettet die Phänomene“ waren häufig Titel und Inhalt seiner zahlreichen Vorträge und Veröffentlichungen. In seinen Seminarien zur Lehrerbildung pflegte er einzelne Themen, wie die Sechseck-Konstruktion im Kreis, die Kugelgestalt der Erde, das Ansaugen der Limonade im Strohhalm, von der scheinbar selbst-verständlichen Gewohntheit zur Frage, ja zum vertrackten Problem und dann zur eigenen selbst-sicheren Erkenntnis zu führen. Seine Leitlinien der Pädagogik hat er meist mit den Stichworten genetisch-sokratisch-exemplarisch markiert.

Die folgende „Miniatur“ geschah – so kann ich es nur bezeichnen – an der Ecole d’Humanité in Goldern (Schweiz) mit einer Gruppe von fünf Schülern (15-16-jährig). Sie ist mit ihrem Frage-Antwort-Spiel von mir bewusst in der stichelnden Frageform des von Platon beschriebenen Sokrates gehalten (z.B. Menon – ein unwissender Sklave erkennt die Methode zur Verdoppelung des Quadrates; schon früh eins der Lieblingsthemen Wagenscheins).
Gleichwohl ist sie kein „Wagenschein-Stück“. Erstens war diese sophistische Frage kein Gegenstand für ihn, zweitens hätte er als Lehrer viel weniger geredet (!). Als später Dank an ihn von einem seiner Gastschüler mag sie herhalten.

———————–

Lehrer: Was ist eigentlich schwerer, ein Kilogramm Blei oder ein Kilogramm Federn?

Schüler: Ein Kilo ist ein Kilo!

L: Das stimmt.

S: Die Federn brauchen nur mehr Platz.

L: Ja, das stimmt auch.

S: Das Blei fühlt sich schwerer an.

L: Ja, aber das meine ich nicht. Ist es gleich schwer, wiegt es dasselbe?

S: Ausprobieren!

L: Wie?

S: Wir nehmen 1 Kilo Blei und 1 Kilo Federn … (?) —-

L: —

S: (Kissenschlachten in Gedanken, schöpferisches Chaos, das im Schweigen versinkt)

L: Machen wir es etwas handlicher, nehmen wir Holz statt Federn. Ist ein Kilo Blei so schwer wie ein Kilo Holz? (Er ist so frei, wie die Schüler, auch gelegentlich Kilo statt Kilogramm zu sagen.)

S: Logo!

L: Und ein Kilo Blei so schwer wie ein Kilogramm Stein?

S: Ja natürlich.

L: Ausprobieren!

– Er hat sich einen Stein und einen Bleiklotz mit praktisch gleicher Masse besorgt, – dass beide nur ungefähr 1 kg Masse haben, ist unerheblich – und legt sie gegenüber auf die Tafelwaage. –

S: Sehen Sie!

L: Nimm sie in die Hand, sind sie gleich schwer?

S: Ja.

L: Und jetzt tauche beide Hände ins Wasser – sind sie gleich schwer?

S: Nein, jetzt ist der Stein leichter als das Blei.

L: Siehst Du!

S: Ja, im Wasser, da ists anders. – Holz wiegt im Wasser gar nichts, das geht sogar nach oben. Wie ein Luftballon!

L: Warum?

S: Weil es leichter ist als Wasser.

L: Und der Stein?

S: Ist schwerer als Wasser, und Blei ist noch schwerer.

L: Denkt dran, von allem ist es ein Kilogramm.

S: Aber sie sind verschieden groß. – Die Dichte ist anders. – Der Auftrieb macht den Stein und das Holz leichter. – Das Blei auch, aber ganz wenig.

L: Und draußen?

S: Gibt es keinen Auftrieb.

L: Und der Luftballon?

S: Ach so…

L: Wenn ich einen Luftballon, oder besser eine leere Plastiktüte mit Luft aufblase, wird sie dann schwerer?

S: Nein.

L: Ist in der vollen Plastiktüte mehr drin als in der leeren?

S: (Gelächter)

L: Hat also die volle Plastiktüte eine größere Masse als die leere?

S: Ja, ein paar Gramm schon. – Das kann man aber nicht wiegen. – Doch, wo es keine Luft hat. – Wasser wiegt im Wasser auch nichts. – Dann platzt aber die Tüte! (Gemeint ist die luftgefüllte Tüte im Vakuum).

L: Was ist schwerer, ein Gramm Blei oder ein Gramm Luft?

S: Die Luft wiegt ja nichts.

L: Was ist schwerer, 10 Gramm Blei oder 10 Gramm Styropor?

S: Im Styropor ist Luft? – Ja. – Ich weiß nicht. – Ist doch egal.

L: Wieso egal?

S: Die Luft wiegt ja nichts. – Wie wollen Sie das Styropor dann überhaupt richtig wiegen? – Ohne Luft. – Wie willst du denn da die Luft rauslassen? – Nein, ich meine im Vakuum. – Verjagts die dann nicht?

L: Ausprobieren!

– Eine Styroporkugel von ca. 10 cm Durchmesser wird unter die Glasglocke der Luftpumpe gelegt. Dann wird das Glas luftleer gepumpt, die heimlich erwartete Katastrophe bleibt aus. –

S: Können Sie die wiegen?

L: Im Vakuum?

S: Ja. – Aber dann auch in der Luft.

– Der Versuch wird mit einer kleinen Schalenwaage, klein genug, um unter die Glasglocke zu passen, groß genug, die Kugel aufzunehmen, durchgeführt. –

L: Und was gilt jetzt? Macht es das Vakuum schwerer oder die Luft leichter?

S: Vakuum ist nichts, kann nichts machen! – Im Wasser stimmts nicht, also kann es in der Luft auch nicht stimmen. – Jedenfalls nicht genau.

L: Was ist also schwerer, ein Kilogramm Blei oder ein Kilogramm Federn?

S: Das Blei, denn es hat weniger Auftrieb in der Luft.

L: Seid Ihr sicher?

S: Doch. – Logo, wir leben ja nicht auf dem Mond!

L: Dann fragt mal zuhause eure Eltern, was sie meinen!

S: Au ja!

Man sieht, eine solche Unterrichtssituation kann sich nur ergeben, wenn die Schüler schon einiges wissen. Über Masse und Gewicht muss schon ausführlich gearbeitet worden sein. Den Auftrieb, zumindest in Flüssigkeiten, müssen sie kennen. Dass Luft eine Masse hat, muss ihnen auch bekannt sein, ebenso die Ohnmacht des Vakuums (Vakuum ist nichts, kann nichts machen!). Dieses Beispiel ist also nicht geeignet, den Unterschied zwischen der Masse und ihrem Gewicht einzuführen, aber dazu, ihn endlich besser zu begreifen. Dass je nach vorhandenem Material (z.B. empfindliche Federwaage) und den spontanen Antworten der Schüler ein anderer Gesprächsverlauf zum Ziel führen muss, versteht sich von selbst. Sicher aber sind derlei Sequenzen in der Sekundarstufe I genauso möglich (und nötig!) wie kurz vor dem Abitur.
Und in einem Physik-Seminar? – Ausprobieren!

Veröffentlicht zum 100. Geburtstag von Martin Wagenschein in:
Physik in der Schule 34 (1996)12 S. 429-430
Pädagogischer Zeitschriftenverlag, Berlin