Aus Quader gebaute Körper – Aufgaben und Lösungen
Zusammengesetzte Körper zu berechnen ist einfach, doch es verlangt Geduld und Konzentration.
Beispiel 1: Würfel auf Quader
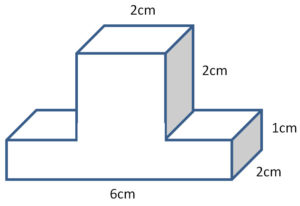
Berechnung der Oberfläche
Überlegung: Wir können die Oberfläche eines Quaders und dann eines Würfels berechnen. Dort, wo der Würfel auf dem Quader steht, wird einerseits beim Quader wie auch beim Würfel eine Fläche der Würfelseite abgedeckt.
Gegeben: a = 6cm, b = 1cm und c = 2cm
Quader Oberfläche: AQ = 2ab + 2ac + 2bc
Würfel Oberfläche: AW = 6c2
Abgedeckte Fläche: AA = 2c2
Total Oberfläche = AQ + AW – AA = 12cm2 + 24cm2 + 4cm2 + 24cm2 – 8cm2 = 56cm2
Berechnung des Volumens
Volumen Quader: VQ = abc = 12cm2
Volumen Würfel: VW = c3 = 8cm3
Volumen insgesamt: V = 20cm3
Beispiel 2
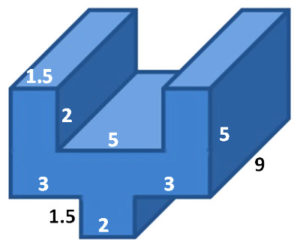
Überlegung zur Oberfläche
Der Körper hat eine identische Vorder- und Rückseite. Sie kann in 4 Rechtecke zerlegt werden, wobei 2 davon identisch sind. Also
A1 = 8cm · 3cm (mittlere Fläche) = 24cm2
A2 = 2cm · 1.5cm (seitliche Flächen, kommen doppelt vor) 2A2 = 6cm2
A3 = 2cm · 1.5cm (untere Fläche) = 3cm2
A Front = 33cm2
A Hinterseite = 33cm2
Die restlichen Flächen haben alle die gleiche Höhe (nämlich hier 9cm). Sie können zu einem grossen Rechteck auseinandergefaltet werden:
A = 9cm (1.5 + 3 + 5 + 1.5 + 2 + 5 + 2 + 1.5 + 5 + 3 + 1.5 + 2)cm = 9cm ⋅ 33cm = 297cm2
Front, Rückseite und Manschette addiert:
A Total = 33cm2 + 33cm2 + 297cm2 = 363cm2
Überlegung zum Volumen
Der Körper hat eine Tiefe von 9cm. Das Volumen also erhalten wir, indem wir die Frontfläche mit der Tiefe multiplizieren.
V = A Front ⋅ Tiefe = 33cm2 ⋅ 9cm = 297cm3
Beispiel 3
Folgender Block hat zwei runde Löcher. Die Aussparungen sind Zylinder.
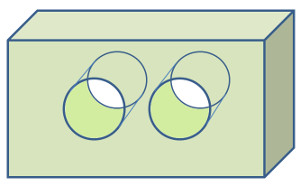
Höhe a = 5cm
Breite b = 4cm
Tiefe c = 6cm
Durchmesser Loch
d = 2cm
Überlegungen zur Oberfläche
Zuerst die Oberfläche des Quaders berechnen.
Abgezogen werden 4 Kreisflächen.
Dazu kommt die innere Oberfläche. Diese ist rechteckig (Tiefe c x Kreislinie).
Oberfläche Quader A Quader = 148cm2
Kreisoberfläche A Kreis = 3.14cm2 (diese Fläche muss 4-Mal abgezogen werden).
Innere Oberfläche A innere = 2cm ⋅ 3.14 = 6.28cm2 (diese Fläche gibt es zwei Mal).
Total A = A Quader – 4 ⋅ A Kreis + 2 ⋅ A innere = 173.133cm2
Berechnung des Volumens
Vom Volumen des Quaders werden zwei Zylinder abgezogen.
V Quader = 120cm3
V Zylinder = 2 ⋅ 3.14 ⋅ 6cm = 37.699cm3
V Total = 157.699 cm3