Als Beispiel: Zentrische Streckung eines Vierecks

Von einem Streckungszentrum S führen Strahlen zu den Eckpunkten einer Fläche. Soll diese Fläche vergrössert werden, müssen die Strahlen verlängert werden um einen gegebenen Faktor. Dieser Faktor heisst k = Streckungsfaktor.

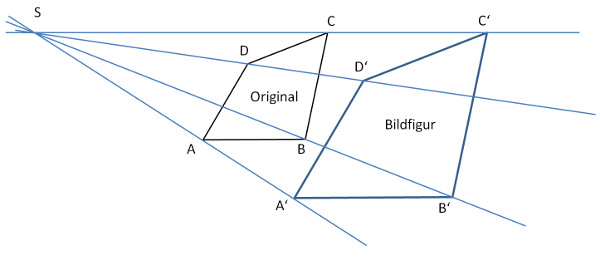
Der Streckungsfaktor k

Der Streckfaktor k ist definiert wie folgt:

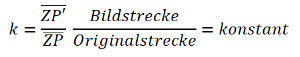
Das heisst: der Streckungsfaktor k ist definiert durch das Verhältnis der Bildstrecke zur Originalstrecke. In der obigen Abbildung könnte das zum Beispiel ZA‘ : ZA sein.

Folgendes gilt für den Streckungsfaktor:

k > 1    Vergrösserung zu einem ähnlichen grösseren Bild
k = 1    identisches Bild
k < 1    Verkleinerung zu einem ähnlichen kleineren Bild
k = 0    Verkleinerung zu einem Punkt
k nagativ    Punktspiegelung zu einem ähnlichen Bild auf der anderen Seite von S.

Eigenschaften von Original und Bildfigur

• Die Seiten von Bildfigur und Original sind immer parallel.
• Die entsprechenden Punkte von Bildfigur und Original liegen immer auf einer Gerade, die durch das Streckzentrum führt.
• Die Strecken der Bildfigur sind um k grösser bzw. kleiner als die Strecken des Originals.
• Die Fläche der Bildfigur ist um k² grösser bzw. kleiner als die Fläche des Originals

Aufgabentypen

Um Aufgaben der Zentrischen Streckung zu lösen, muss ein grosser Lineal und ein (Geo-)Dreieck oder zwei Dreiecke vorhanden sein.

Gegeben eine Originalfigur, das Streckungszentrum S und ein Streckungsfaktor.
Gesucht die Bildfigur

Gegeben ein Original und ein Bildfigur.
Gesucht das Streckungszentrum S und Streckungsfaktor k.

Gegeben ein Punkt der Bildfigur, alle Punkte des Originals und Streckungszentrum S.
Gesucht Bildfigur und Streckungsfaktor.