Zahlensysteme liegen einer Kultur zugrunde. Wohl wegen unseren 5-strahligen Händen ist das 10-er-System weit verbreitet. Doch wir finden in der Vergangenheit auch 6-er Systeme.
In der Gegenwart, aufgrund der technischen Entwicklung mit Strom (Computer) wurde vor allem das Binärsystem wichtig. Aufbauend auf das Binärsystem ist das Hexigesimalsystem.
Das Dezimalsystem (Basis ist 10)
Wir sind uns gewohnt, im Zehnersystem zu rechnen, d.h. mit unseren 10 Ziffern stellen wir alle Zahlen dar.
Sind alle Ziffern (Zeichen) „aufgebraucht“, wird links von der Ziffer eine nächste gesetzt, beginnend wieder bei 0. Mit zwei Ziffern lassen sich 100 Zahlen bilden).
0 10 20 30 40 50 60 70 80 90
1 11 21 31 41 51 61 71 81 91
2 12 22 32 42 52 62 72 82 92
3 13 23 33 43 53 63 73 83 93
4 14 24 34 44 54 64 74 84 94
5 15 25 35 45 55 65 75 85 95
6 16 26 36 46 56 66 76 86 96
7 17 27 37 47 57 67 77 87 97
8 18 28 38 48 58 68 78 88 98
9 19 29 39 49 59 69 79 89 99
Das Dezimalsystem ist ein Stellenwertsystem.
2’583 bedeutet also:
2’583 3 gehört zu den Einsern
2’583 8 gehört zu den Zehnern
2′583 5 gehört zu den Hundertern
2‚583 2 gehört zu den Tausendern
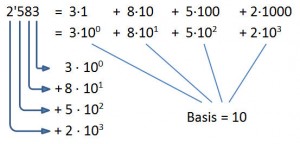
Damit ist 2’583 = 3 + 80 + 500 + 2000
Das Dualsystem oder Binärsystem (Basis ist 2)
Im Zweier- oder Dualsystem gibt es nur zwei Ziffern. Üblicherweise nehmen wir 0 und 1.
Die Zahlen werden genau gleich gebildet wie im Zehnersystem (mit zwei Stellen kann man nur gerade 4 Zahlen bilden).
0000 0001 0010 0100 1000 10000
0011 0101 1001 10001
0110 1010 10010
0111 1011 ...
1100
1101
1110
1111
Das Hexagesimalsystem (Basis ist 16)
Das Hexagesimalsystem hat statt 10 nun 16 Zeichen. Nach 9 folgen die ersten Buchstaben unseres Alphabets. Hier alle 2-stelligen Zahlen (es sind 256). Dieses Zahlensystem spielt im Computer eine Rolle (z.B. die Farbwerte im RGB-System werden so angegeben).
0 10 20 30 ... A0 B0 ... F0 1 11 21 31 ... A1 B1 ... F1 2 12 22 32 ... A2 B2 ... F2 3 13 23 33 ... A3 B3 ... F3 4 14 24 34 ... A4 B4 ... F4 5 15 25 35 ... A5 B5 ... F5 6 16 26 36 ... A6 B6 ... F6 7 17 27 37 ... A7 B7 ... F7 8 18 28 38 ... A8 B8 ... F8 9 19 29 39 ... A9 B9 ... F9 A 1A 2A 3A ... AA BA ... FA B 1B 2B 3B ... AB BB ... FB C 1C 2C 3C ... AC BC ... FC D 1D 2D 3D ... AD BD ... FD E 1E 2E 3E ... AE BE ... FE F 1F 2F 3F ... AF BF ... FF
Übersicht
| 2-er | 3-er | 4-er | …. | …. | 10-er | 12-er | 16-er | |
| 0 1 10 11 100 101 110 111 1000 1001 1010 1011 1100 1101 1110 1111 10000 10001 10010 10011 10100 10101 10110 10111 11000 11001 11010 11011 11100 11101 11110 11111 100000 |
0 1 2 10 11 12 20 21 22 100 101 102 110 111 112 120 121 122 200 201 202 210 211 212 220 221 222 1000 1001 1002 1010 1011 1012 |
0 1 2 3 10 11 12 13 20 21 22 23 30 31 32 33 100 101 102 103 110 111 112 113 120 121 122 123 130 131 132 133 200 |
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 |
0 1 2 3 4 5 6 7 8 9 A B 10 11 12 13 14 15 16 17 18 19 1A 1B 20 21 22 23 24 25 26 27 28 |
0 1 2 3 4 5 6 7 8 9 A B C D E F 10 11 12 13 14 15 16 17 18 19 1A 1B 1C 1D 1E 1F 20 |
Übungen zu den Zahlensystemen
Umrechnungen:
A. Dezimal in binär: 10-er in 2-er
B. Binär in dezimal: 2-er in 10-er
C. Hexadezimal in dezimal: 16-er in 10-er
D. Dezimal in Hexadezimal: 10-er in 16-er
A. Wie kann ich eine Zehnerzahl in eine Dualzahl umwandeln?
50
50 : 2 = 25, Rest 0
25 : 2 = 12, Rest 1
12 : 2 = 6, Rest 0
6 : 2 = 3, Rest 0
3 : 2 = 1, Rest 1
1 : 2 = 0, Rest 1
Die Dualzahl von 50 heisst also im Binärsystem: 110010
B. Wie kann ich eine Dualzahl (Binärzahl, Zweierzahl) in eine Zehnerzahl umwandeln?
1 1 0 0 1 0
25 24 23 22 21 20
32 16 8 4 2 1
= 1*32 + 1*16 + 0*8 + 0*4 + 1*2 + 0*1 = 50
C. Hexadezimalzahl16 in dezimal10
FF132B16
= B ⋅ 160 + 2 ⋅ 161 + 3 ⋅ 162 + 1 ⋅ 163 + A ⋅ 164 + A ⋅ 165
= 11 ⋅ 160 + 2 ⋅ 161 + 3 ⋅ 162 + 1 ⋅ 163 + 15 ⋅ 164 + 15 ⋅ 165
= 11 ⋅ 1 + 2 ⋅ 16 + 3 ⋅ 256 + 1 ⋅ 4’096 + 15 ⋅ 65’536 + 15 ⋅ 1’048’576
= 11 + 32 + 768 + 4’096 + 983040 + 15’728’640
= 16’716’58710
D. Dezimal in Hexadezimal
555510 in eine Hexadezimale Zahl umwandeln:
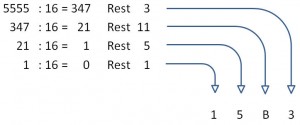
Die hexadezimale Zahl heisst: 15B316
Weitere Übungen und Fragen
- Wie gross ist der Informationsgehalt einer 6-stelligen Binärzahl?
Maximal kann mit 6 Stellen die Zahl 111111 geschrieben werden.
Sie ist im Zehnersystem: 20 + 21 + 22 + 23 + 24 + 25 = 1 + 2 + 4 + 8 + 16 + 32 = 63 + der Wert 0 = 64
2.