Vigenère-Chiffre brechen ohne Schlüssel – die Kasiski-Methode

Wie kann eine Vigenère-Chiffre ohne Schlüssel dechiffriert werden?

Vigenère-Chiffre war lange Zeit nicht knackbar. Auf der Seite zur Vigenère-Verschlüsselung haben wir gesehen, dass mit Brute-Force bei einer Schlüssellänge von 5 sind es bereits über 12 Millionen Möglichkeiten, die der Reihe nach ausgetestet werden müssen. Nun wollen wir die Vigenère-Chiffre brechen, ohne den Schlüssel zu kennen.

Was aber, wenn wir den Schlüssel nicht kennen?

Wir teilen das Problem in verschiedene Teilfragen auf.

  1. Wie viele Buchstaben enthält das Schlüsselwort? Wir versuchen, die Schlüssellänge herauszufinden.
  2. Wie lauten die Buchstaben des Schlüssels.

Friedrich Wilhelm Kasiski (1805 – 1881) veröffentlichte 1863 in seinem Buch Die Geheimschriften und die Dechiffrir-Kunst einen Test zur Kryptoanalyse der Vigenère-Chiffre, der noch heute als Kasiski-Test bekannt ist. Das Verfahren, das Kasiski verwendete, konnte die Schlüsselwortlänge dieser Chiffre ermitteln.

Die Kasiski-Methode in Kürze

Folgendes hat Kasiski festgestellt:

  • Es gibt gemeinsame Di- und Trigramme im Klartext
  • Einige n-Gramme haben gerade die Distanz von einem Vielfachen des gewählten Schlüsselwortes
  • Das bedeutet, dass diese n-Gramme in derselben Weise verschlüsselt werden

Daraus hat er das folgende Vorgehen vorgeschlagen:

  • Suche gleiche n-Gramme im Chiffre-Text
  • Bestimme die Distanz zwischen ihnen
  • Diese Distanz kann einem Vielfachen der Schlüssellänge entsprechen.

Schlüssellänge (Kasiski) am Beispiel sorgfältig und Schritt für Schritt erklärt

Damit wir die Vigenère-Chiffre brechen können nehmen wir einen Text von Simon Gfeller, der vigenère-verschlüsselt wurde.

JJVSLRUCJVVDKVYJPWPLVOSVTNLSAHLPCARXFPWXEVNQMNSWVOSIXSIZSFXWTGYKSKLFRRKMICRIIAJGVEYEJXGSWIEJJVEPIZTJWYLGYSNXELKJCTLWRIDAYHPXHFXKILLVJZJXEPRQAFQCFITQJRSTRXOMQPTRNUMPRPJLKQPEPVIKNWPDETQZROOMVXJGSEIJIMALYKDASXPCHVTBEPSVJIMEQEIEQSSEPRJZTGVOIECJMNSIELNPKSYKNFXEPIIYNGSFQLTIYXXMKRTIHPRQGMRMWYVZJRMPWKKHOEFRUJNIRCELKSEFRIEHQMEKXVTKVTDGYASHWFWKOLEFDHVSXSYYKVHWEPFRKKSKPDMTNYLPCELYJWHLVBUJWEWMTNEYHLRUKWRLYHZKXIXDSETJRSPPCKSQTWHNGWQPYJIAJLWTRXYYERPYEJGYNSIINFXEPHZKXALYHVXLPFPGBOSZZWPVTEYPRIEMJRZDWVTSYYXEYTYIYTLEYJMYPPVOXIMCIETJROPRWAXWDZLCKSHLDWVYEITEWVOEYXLYJXZLPYHVXBIRCEZTQSNVXVFZQLMWZZEIYFRUHZGSPVNGWJDTGYOSWRCYVTJKCLWJIMSMDMTNIIYCIZYJWLNOSKVYPXYEZJVOPREGHOPYHVNSXPFRUYYVPNOKKXMNSYEJQENSXVBJVRYYVMYMYDMTNMMYPME

 

verschluesselter text mtn

Das 3-Gramm MTN kommt 4 Mal vor in der Chiffre.
Die Positionen sind: 363, 384, 622, 699.
Daraus können die Distanzen zwischen den gleichen n-Grammen berechnet werden.
Von diesen Distanzen können die Primfaktoren gebildet werden, um die mögliche Schlüssellänge zu finden. Hier kann leicht die 7 als Schlüssellänge erkannt werden.

Distanzen Primfaktoren
2 3 5 7 11 13 17 19 23 n
384 – 363 = 21 3 7
622 – 384 = 238 2 7 17
622 – 363 = 259 7 37
699 – 622 = 77 72
699 – 384 = 315 32 5 7
699 – 363 = 336 24 3 7

Es gibt Online-Tools, welche uns die Arbeit abnehmen.

Mit dem Tool von Brian kann folgendes Resultat gewonnen werden:

Distanz             
 Häufigkeit der Faktoren
2 35
3 19
4 22
5 14
6 11
7 63
8 10
9 8
10 6
11 7
12 7
13 5
14 31
15 5
16 5
17 6
18 4
19 1
20 4

Herausfinden des Schlüssels

Wenn wir nun wissen, wie lang das Schlüsselwort ist, können wir folgende Eigenschaft nutzen: Wenn n die Schlüssellänge ist, dann wird jeder n+1-Buchstabe mit dem gleichen Alphabet verschlüsselt. Wenn wir also den Cipher-Text in n lange Blöcke unterteilen, dann können wir die Buchstabenhäufigkeit von jedem Buchstaben untersuchen, welcher mit dem gleichen Schlüsselwort-Buchstaben verschlüsselt worden ist.

chiffre in bloecken

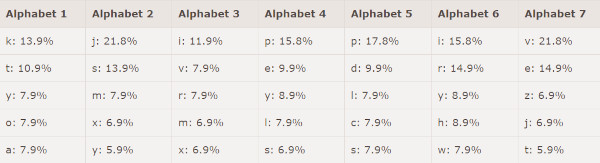
Alle Buchstaben, welche mit dem ersten Schlüsselwort-Buchstaben (dem 1. Alphabet) verschlüsselt worden sind, habe ich hier orange umrandet. Wir schreiben sie raus und bestimmen für alle 7 Alphabete die Häufigkeit. Ein Vergleich mit der Buchstabenhäufigkeit der deutschen Sprache zeigt uns, welcher Buchstabe das E ist.

buchstabenhäufigkeit der alphabete

Damit nun entschlüsseln wir das Schlüsselwort.

  1. Alphabet: K kommt am häufigsten vor, entspricht also dem E, also ist der erste Buchstabe G

 

Zurück zur Vigenère-Verschlüsselung

 

Nützliche Links

https://www.guballa.de/vigenere-solver

https://www.dcode.fr/vigenere-cipher

https://asecuritysite.com/encryption/kasiski

https://www.boxentriq.com/code-breaking/vigenere-cipher

https://www.simonsingh.net/The_Black_Chamber/vigenere_cracking_tool.html

https://crypto.interactive-maths.com/kasiski-analysis-breaking-the-code.html