Textgleichungen sind für die meisten SchülerInnen zu Beginn meist schwierig. Aber sie werden einfach, wenn Du gewisse Punkte befolgst – und hartnäckig bleibst.
Das hilft dir beim Lösen von Textgleichungen:
- Zuerst einmal: Lies den Text sorgfältig durch!
- Unterstreiche die Textstellen, die exakte Angaben machen (wie „das Dreifache“ oder Zahlen und was sie bezeichnen).
- Formuliere die Aufgabe in Deinen eigenen, einfachen Worten.
- Finde heraus, nach was Du suchen musst.
- Nun schreibe heraus, was gegeben ist und was gesucht ist, am besten mit den Variablen.
- Mach Dir wenn immer möglich eine Skizze von der Situation.
- Suche nach den Formeln und Gesetzen, die Dir helfen könnten, die Aufgabe zu lösen.
- Stelle die Gleichung auf.
- Löse die Gleichung durch Äquivalenzumformungen.
- Kontrolliere die Lösung durch Probe (Einsetzen des Ergebnisses).
- Formuliere einen Antwortsatz (jede Textaufgabe erfordert eine Textantwort!).
Vorgerechnete und erklärte Beispiele
Einfache Textgleichung 1
Das Dreifache einer Zahl gibt genau 12. Wie heisst die Zahl?
Übersetzung der Textangabe in eine Gleichung:
3 ⋅ x = 12
Lösung der Gleichung
3 ⋅ x = 12 | :3
x = 4
Die Zahl heisst 4.
Einfache Textgleichung 2
Das Fünffache einer Zahl vermehrt um 7 ergibt 32. Wie heisst die Zahl?
5 ⋅ x + 7 = 32
Lösung der Gleichung
5 ⋅ x + 7 = 32 | -7
5x = 25 | : 5
x = 5
Die Zahl heisst 5.
Einfache Textgleichung 3
Das Neunfache einer Zahl vermindert um 13 ergibt 23.
9 ⋅ x – 13 = 23
Lösung der Gleichung:
9 ⋅ x – 13 = 23 | +13
9x = 36 | : 9
x = 4
Die Zahl heisst 4.
Einfache Textgleichung 4
Wenn man eine Zahl um 2 vermindert und das Fünffache davon nimmt, bekommt man 20.
5 ⋅ (x – 2) = 20
Lösung der Gleichung:
5 ⋅ (x – 2) = 2 | umf.
5x – 10 = 2 | + 10
5x = 12 | : 5
x = 12/5 = 2.4
Die Zahl ist 2.4.
Einfache Textgleichung 5
Das Doppelte einer Zahl vermehrt um 8 ergibt die Gegenzahl vermindert um 1.
2 ⋅ x + 8 = – x – 1
Lösung der Gleichung:
2 ⋅ x + 8 = – x – 1 | +x
3x + 8 = – 1 | – 8
3x = – 9 | : 3
x = – 3
Die Zahl heisst – 3.
Einfache Textgleichung 6
Das Produkt einer Zahl und 5 ergibt 70.
5x = 70
5x = 70 | :5
x = 13
Die Zahl heisst 13.
Einfache Textgleichung 7
Die Summe zweier aufeinanderfolgender natürlicher Zahlen ist 27.
x + (x + 1) = 27
2x + 1 = 27
2x = 26
x = 13
Die Zahl heisst 13.
Einfache Textgleichung 8
Die Differenz einer Zahl mit einem Viertel der Zahl ergibt 15.
x – x/4 = 15
3x/4 = 15
3x = 60
x = 20
Die Zahl heisst 20.
Einfache Textgleichung 9
Das um 6 vermehrte Produkt einer Zahl mit 5 ergibt 41.
5x + 6 = 41
5x = 35
x = 7
Die Zahl heisst 7.
Einfache Textgleichung 10
In 17 Jahren ist Monika doppelt so alt wie sie es jetzt ist.
x + 17 = 2x I – x
x = 17
Sie ist jetzt 17 Jahre alt.
Einfache Textgleichung 11
Verdreifache ich eine Zahl, so erhalte ich die um 8 vergrösserte Zahl.
3x = x + 8
2x = 8
x = 4
Die Zahl heisst 4.
Einfache Textgleichung 12
Multipliziere ich eine Zahl mit sich selber, so erhalte ich 121.
x ⋅ x = 121
x = 11
Die Zahl heisst 11.
Einfache Textgleichung 13
Addiere ich zu einer Zahl das Produkt aus 5 und 3, so erhalte ich diese Zahl um
10 vergrössert.
x + 5 ⋅ 3 = x + 10 I – x
15 = 10 ist ein Widerspruch.
Diese Aufgabe ist nicht lösbar.
Weitere schwierigere Aufgaben
Beispiel 1: Nussaufgabe
Susanne und Anna haben zusammen 600 Nüsse gesammelt. Anna sagt: Wenn du mir die Hälfte der Nüsse gibst, die du hast, und ich dir darauf einen Drittel der Nüsse gebe, die ich dann habe, so besitzen wir gleich viele Nüsse. Wie viele Nüsse besassen beide am Anfang?
x + y = 600 Nüsse
x + 600 – x = 600 Nüsse
Susanne gibt Anna die Hälfte, Anna bekommt die Hälfte.
Susanne Anna
x – x/2 600 – x + x/2
x/2 600 – x/2
Anna gibt Susanne einen Drittel zurück. Dann sollen es bei beiden gleich viele sein.
x/2 + 200 – x/6 = 400 – 2x/6
2x/6 + 200 = 400 – x/3
x/3 + x/3 = 400 – 200
2/3 x = 200
2x = 600
x = 300
Also hatten auch am Anfang beide gleich viele Nüsse, nämlich je 300.
Beispiel 2: Viererzahlen
Fünf aufeinander folgende Viererzahlen geben zusammen 420. Wie heissen sie?
Gegeben
Fünf Zahlen
aufeinanderfolgende Viererzahlen
ihre Summe ist 420
x + (x+4) + (x+8) + (x+12) + (x+16) = 420
5x + 40 = 420
5x = 420 – 40 = 380
x = 76
Probe: 76 + 80 + 84 + 88 + 92 = 420 q.e.d.
Die erste Zahl heisst 76.
Beispiel 3: Mathematischer Term in Worten
Die Differenz der Quadrate von zwei natürlichen Zahlen mit dem Unterschied 3 beträgt 381. Wie heisst die kleinere der beiden Zahlen?
Was ich daraus lese:
Differenz ist die eine Zahl von der anderen abgezogen, subtrahiert
Quadrat heisst Zahl mal Zahl
natürliche Zahlen sind die Zahlen, mit denen wir zählen, also 1, 2, 3, 4…
Unterschied 3 bedeutet: es hat zwischen der ersten und der zweiten Zahl einen Unterschied von 3
Gefragt ist nach der kleineren der beiden Zahlen.
(x + 3)2 – x2 = 381
x2 + 6x + 9 – x2 = 381
6x + 9 = 381
6x = 372
x = 62
Die kleinere Zahl ist 62.
Beispiel 4: Weg – Zeit – Geschwindigkeitsaufgabe
Zwei Fahrzeuge kommen mit den Geschwindigkeiten 40 und 60 km/h von zwei Orten, die 50 km voneinander entfernt sind, einander entgegen. Dabei fährt das zweite 30 Minuten nach dem ersten ab. Bestimme, wann und wo sie sich treffen.
Was ich aus dem lesen kann:
Fahrzeug A hat 40km/h
Fahrzeug B hat 60km/h
Distanz der Abfahrt 50km
B fährt 30 Minuten später ab
Gesucht: Wann und wo sie sich treffen
Ich erstelle daraus zwei Gleichungen:
Fahrzeug A: y = 40x
Fahrzeug B: y = – 60 (x – 0.5) + 50
Gleichsetzung der Gleichung:
40x = – 60 (x – 0.5) + 50
40x = – 60x + 30 + 50
100x = 80
x = 80/100 = 0.8
Sie treffen sich nach 0.8 Stunden oder 48 Minuten.
Einsetzen von x in die Gleichung für Fahrzeug A:
y = 40 ⋅ 0.8 = 32
Sie treffen sich 32 Kilometer vom Abfahrtsort von Fahrzeug A (oder 18 Kilometer vom Abfahrtsort von Fahrzeug B).
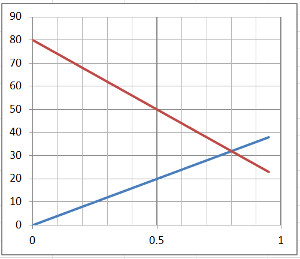
Ich kann die Aufgabe auch grafisch lösen.
Die y-Achse stellt dann den Weg dar,
die x-Achse stellt die Zeit dar.
Die Fahrzeuge beschreiben Geraden im Koordinatensystem.
Fahrzeug A ist durch die blaue Gerade dargestellt.
Fahrzeug B durch die rote Gerade. Es fährt 30 Minuten (0.5 Stunden) später von genau 50km Entfernung aus los.
SMS-Aufgabe
Max und Roger prahlen mit der Menge SMS, die sie Tag für Tag versenden. Max hat gestern 25 SMS verschickt. Das sind 7 SMS mehr als die dreifache Menge von Roger. Wie viele SMS hat Roger gestern verschickt?
Lösung:
Max hat gestern 25 SMS gesendet. Sieben mehr als die dreifache Menge von Roger.
Roger hat x SMS gesendet. 3x + 7 entspricht also Maxens Anzahl.
25 = 3x + 7
3x = 25 – 7
18 = 3x
x = 6
Roger hat also 6 SMS versendet.
Kontrolle:
6 * 3 = 18 Max versendet drei mal mehr…
18 + 7 = 25 Max versendet 7 weniger als dreimal mehr….
Weitere SMS-Aufgabe
Max bezahlt mit seinem Handy-Abo 15 Rappen pro SMS. Roger bezahlt nur 5 Rappen pro SMS, dafür eine monatliche Grundgebühr für die SMS-Option von 3 Franken. Ab wie vielen SMS lohnt sich die SMS-Option für Roger?
Lösung:
Max 15 Rappen pro SMS
Roger 5 Rappen pro SMS plus monatliche Grundgebühr von 3 Franken.
0.15 * x = 0.05 * x + 3
x ist die Anzahl SMS. Wichtig ist es, dass gleiche Einheiten verwendet werden: Franken.
Wenn die SMS-Kosten in einer Gleichung einander gleichgesetzt werden, bedeutet x die Anzahl SMS bei denen die beiden gleich viel bezahlen. Wir lösen nach x auf:
0.15x – 0.05x = 3
0.1x = 3
x = 30
Das heisst, ab dem 31. SMS wird Roger profitieren.
Bei 30 SMS zahlen sie beide gleich viel.
Kontrolle:
Max im Monat: 30*0.05 + 3 = 4.50
Roger im Monat: 30*0.15 = 4.50
Treppen- und Stufenaufgabe
3. Eine Treppe hat 22 Stufen. Würde jede Stufe um 1.6 cm höher gebaut, könnten zwei Stufen eingespart werden. Wie hoch ist eine Stufe?
Schritt 1 Lies den Aufgabentext sorgfältig durch!
Für eine Treppe, welche eine vorgegebene Höhe überwinden soll, gilt: Je höher die einzelnen Stufen sind, desto weniger Stufen enthält die Treppe.
Schritt 2 Wahl der Unbekannten
Jede Stufe ist x cm hoch.
Mit anderen Worten: x = Höhe einer Stufe in cm
Schritt 3 Aufstellen der Gleichung
Höhe der Original-Treppe = Höhe der geänderten Treppe (in cm)
Wir können die Höhe der Treppe auf zwei Arten berechnen. Einerseits mit den 22 vorhandenen Stufen, andererseits mit den 20 höheren Stufen:
Gleichung: 22 * x = 20 * (x + 1.6cm)
Schritt 4 Lösen der Gleichung
22x = 20x + 32cm
22x – 20x = 32cm
2x = 32cm
x = 16cm
Die Höhe der Treppenstufe x beträgt also 16cm
Schritt 5 Prüfen der Lösung
Wir rechnen nach: 22 Stufen zu 16 cm ergeben eine Höhe von 22 * 16 cm = 352 cm
20 Stufen zu (16 + 1.6) cm ergeben eine Höhe von 20 * 17.6 cm = 352 cm
Schritt 6 Textantwort
Jede Stufe ist 16 cm hoch.