Ein Beispiel:
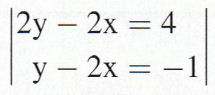
Die beiden Gleichungen können als lineare Funktionen gesehen werden.
Es gibt grundsätzlich 3 Möglichkeiten der Lösungsmenge:
- Die beiden Geraden haben einen Schnittpunkt (einen gemeinsamen Punkt). In diesem Fall haben sie eine Lösung.
- Die beiden Geraden sind parallel, d.h. sie schneiden sich nie und es gibt keine Lösung. Die Lösungsmenge ist leer.
- Die beiden Geraden liegen aufeinander, sind identisch. Es gibt unendlich viele Lösungen.
Die Vorgehensweise, um ein Gleichungssystem zu lösen, sind die folgenden:
A. Additions– oder Subtraktions–Verfahren
B. Einsetzungsverfahren
C. Gleichsetzungsverfahren
Du suchst ein Verfahren aus, welches eine der beiden Variablen (Unbekannten) eliminiert. Grundsätzlich kannst du jedes Verfahren anwenden, doch die richtige Wahl kann dir das Leben erleichtern…
Gleichsetzungsverfahren
y – x = 2 Gleichung (beide Seiten) durch 2 geteilt
y – 2x = –1
y = x + 2
y = 2x – 1
x + 2 = 2x – 1 gleichsetzen
x – 2x = –1 – 2
–x = –3
x = 3 x-Lösung einsetzen in eine der beiden ursprünglichen Gleichungen
y = 3 + 2
y = 5
Lösung: x = 3 und y = 5
Einsetzungsverfahren:
2y – 2x = 4
y – 2x = –1 umformen
y = 2x – 1
Diese zweite Gleichung setze ich in die erste ein.
2(2x – 1) – 2x = 4
4x – 2 – 2x = 4
2x = 6
x = 3 x in eine der beiden ursprünglichen Gleichungen einsetzen.
y = 2*3 – 1
y = 5
Additionsverfahren
2y – 2x = 4
y – 2x = –1
Ich ziehe die zweite Gleichung von der ersten ab.
2y – y – 2x + 2x = 4 – (–1)
y = 5 Diesen y-Wert in eine der Gleichungen einsetzen
5 – 2x = –1
–2x = – 6
2x = 6
x = 3
Wir haben gesehen, dass wir mit den drei Verfahren immer die selben Lösungen erhalten.
Beispiel einer grafischen Lösung
![]()
beide Gleichungen nach y auflösen:
2x + y = 1 | – 2x
y = – 2x + 1 (lineare Gleichung 1)
– x + y = – 2 | + x
y = x – 2 (lineare Gleichung 2)
Gleichung 1
Steigung m = –2
y-Achsenabschnitt b = 1
Gleichung 2
Steigung m = 1
y-Achsenabschnitt b = – 2
Nun zeichnen wir die Graphen ins Koordinatensystem:
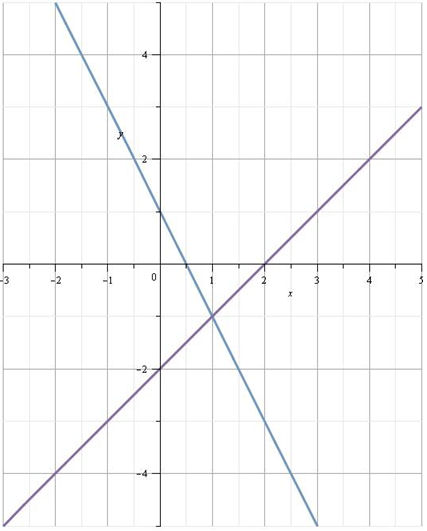
Die Lösungen sind der Schnittpunkt der Geraden und hier direkt ablesbar:
L (x = 1; y = –1)