Der Strahlensatz beschreibt Gesetzmässigkeiten der Streckenverhältnisse (Proportionen) von durch Parallelen (e und f) geschnittene Strahlen mit dem Strahlenzentrum S.

Formeln der drei Strahlensätze

1. Strahlensatz (nur Strahlenabschnitte)

Der erste Strahlensatz besagt, dass das Verhältnis a : (a + b) gleich gross ist wie c : (c + d).

 

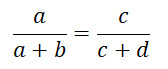
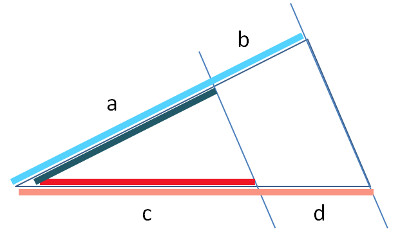
2. Strahlensatz (Strahlenabschnitte und Parallelenabschnitte)

Der zweite Strahlensatz besagt, dass das Verhältnis e : f gleich gross ist wie a : (a + b)

 

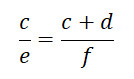
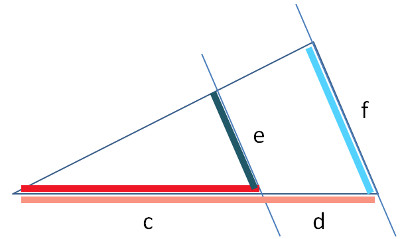
3. Strahlensatz (nur Parallelenabschnitte)

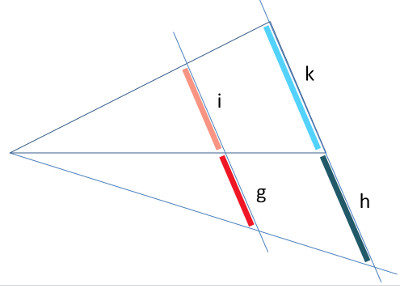
Der dritte Strahlensatz besagt, dass folgendes gilt (siehe Abbildung unten)
g : i = h : k
oder
g : (g + i) = h : (h + k)
oder
i : (g + i) = k : (h + k)

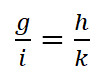
Durchgerechnete Beispiele

Beispiel 1

1. Berechne x und y.

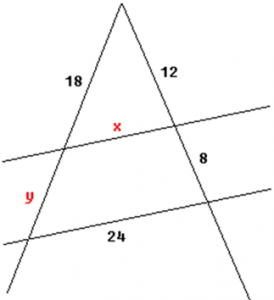Berechnen von x x / 12 = 24 / 20 beide Seiten mit 12 multiplizieren x = 14.4 Berechnen von y (y + 18) : 18 = (12 + 8) : 12 y + 18 = 30 y = 12

Beispiel 2

Es soll die Länge eines Sees (CE = x) bestimmt werden.

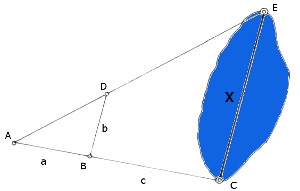
Wir kennen:

a = 25m
b = 45m
c = 80m

 

 

Wir wenden den 2. Strahlensatz an:

x : (a + c) = b : a

um den Nenner zu entfernen und x zu isolieren, müssen beide Seiten mit (a + c) multipliziert werden. Also beide seiten mit 105m multiplizieren.

x = 45 · 105 : 25 = 189m

Die Seebreite ist also 189 Meter.

Weitere Aufgaben mit Lösungsweg

Aufgabe 1

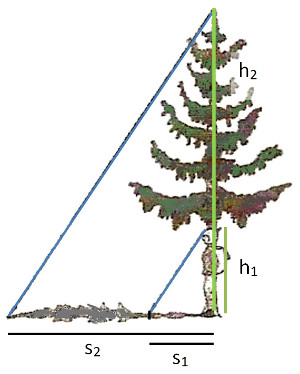
s₁ = 3m
s₂ = 17m
h₁ = 1.8m

 

 

Lösung

Wir wenden den 1. Strahlensatz an, da nur die Strahlen betroffen sind.

Gesucht ist h₂, also

h₂/s₂ = h₁/s₁

Wir multiplizieren beide Seiten mit s2, um h2 zu isolieren:

h₂ = h₁ · s₂ : s₁ = 1.8m · 17m : 3m = 10.2m

Die Tanne hat also eine Höhe h₂ von 10.2 Meter.

Aufgabe 2

In der untenstehenden Aufgabe muss wieder eine Seebreite bestimmt werden.

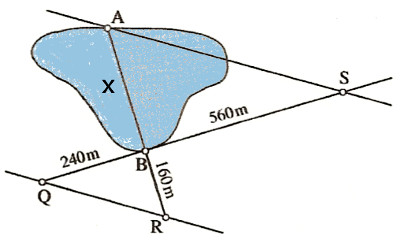
Lösung

Folgende Verhältnisse der Hilfsstrecken sind nützlich (1. Strahlensatz):

x : 560 = 160 : 240

multipliziert mit 560m ist x isoliert:

x = 160 · 560 : 240 = 373.33m

Die Seebreite ist also 373m

Aufgabe 3

Weiter sollen im folgenden Schema b berechnet werden.

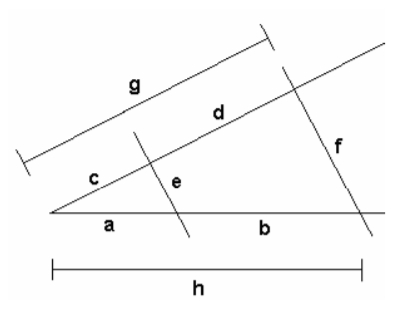
Gegeben sind die Stücke:

a = 5 cm
c = 4 cm
d = 7 cm

Lösung

mit dem 1. Strahlensatz

a : c = (a + b) : (c + d)
5 : 4 = (5 + b) : 11

Um b zu isolieren, müssen beide Seiten mit 11 multipliziert werden:

5 + b = 5 · 11 : 4

b kann bestimmt werden, wenn noch auf beiden Seiten 5 subtrahiert wird:

b = 13.75 – 5 = 9.75

Aufgabe 4

Wie gross ist die Breite des Flusses, wenn c = 45m, b = 28m und d = 61m ist?

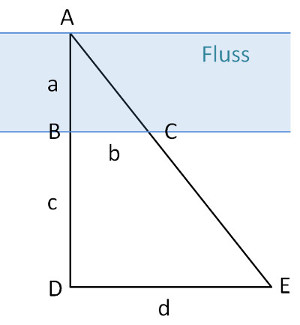
(a + c) : d = a : b

(a + 45) : 61 = a : 28

beide Seiten mit 61 und 28 multiplizieren

28 (a + 45) = 61a
28a + 1260 = 61a

auf beiden Seiten 28a subtrahieren

33a = 1260

a = 38.18m

Der Fluss hat eine Breite von 38.18m.

 

Aufgabe 5

Zwei senkrecht stehende Stäbe a und b stehen wie in untenstehender Abbildung nebeneinander. a = 4cm und b = 10cm. Wie gross ist x beim Kreuzpunkt?

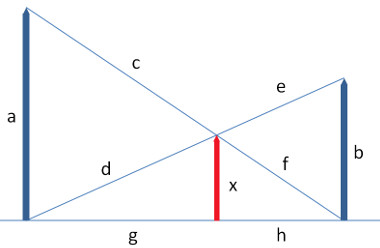
Folgende Verhältnisse können formuliert werden:

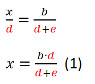
Weiter:

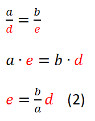
Einsetzen von (2) in (1)

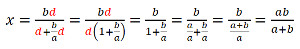
Werte einsetzen:

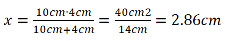
Aufgabe 7

Die Spitzen der beiden Stäbe c und d in eine Linie gebracht, kann in der Verlängerung gerade die Turmspitze anvisiert werden. Wie hoch ist der Turm?

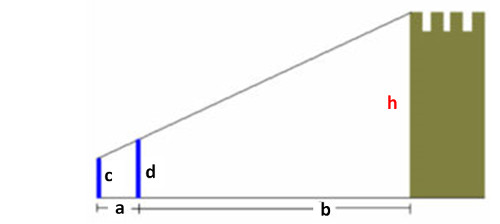
Gegeben:

a = 2m
b = 35m
c = 1.5m
d = 2.4m

Gesucht: h Turmhöhe

 

Diese Aufgabe lässt sich auf zwei Arten lösen.

a) Ziehen wir eine waagrechte Hilfslinie auf der Höhe des kleineren Stockes c, lässt sich leicht der 2. Strahlensatz anwenden:

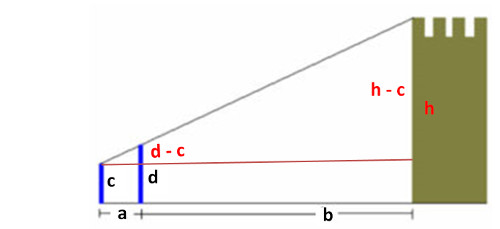
(h – c) : (a + b) = (d – c) : a

eingesetzt:

(h – 1.5) : 37 = 0.9 : 2

Wir multiplizieren die Gleichung mit 37.

h – 1.5 = 37 · 0.9 : 2 = 16.65 m

Nun addieren wir die abgezogene Höhe c wieder dazu:

h = 18.15m

Die Turmhöhe ist h = 18.15m

b)

Die Strahlen werden nach links bis zum Streckungszentrum verlängert:

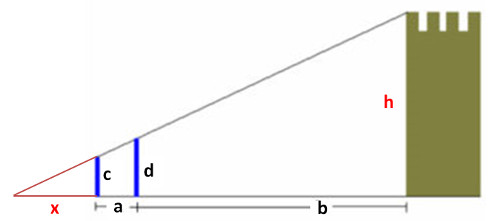
Nun wird in einem ersten Schritt x berechnet (mit dem 2. Strahlensatz):

x : c = (x + a) : d

x = 3.333m

Danach lässt sich mit dem 2. Strahlensatz einfach die Höhe h berechnen:

h : 40.3333 = 1.5 : 3.333

h = 18.15m