Die Prozentrechnung ist eine der häufigsten Anforderungen für Schüler und Lehrlinge. Hier soll zuerst eine kurze Theorie über sie gegeben werden, am Schluss folgen Übungen mit Lösungen dazu.
1% ist der hundertste Teil des Ganzen (von 100%)
0.01 ist der hundertste Teil des Ganzen (von 1)
Die Dezimalzahlen 0,1, 0,5 oder 0,9 gibt einen Bruchteil eines Ganzen an. Eine Prozentangabe ist das 100-fache einer Dezimalzahl, mit einem Prozentzeichen dahinter. Oder umgekehrt: Eine Prozentangabe durch 100 geteilt ergibt die Dezimalzahl. Die folgenden Beispiele verdeutlichen dies:
Dezimalzahl in Prozentangabe umwandeln:
- Kommazahl: 1,00 => 100%
- Kommazahl: 0,99 => 99%
- Kommazahl: 0,33 => 33%
- Kommazahl: 0,00 => 0%
Es ist also ganz simpel: Die Kommazahl mit 100 multiplizieren ergibt die Prozentangabe.
Prozentangabe in Dezimalzahl wandeln:
- Prozentzahl: 100% => 1
- Prozentzahl: 80% => 0,8
- Prozentzahl: 10% => 0,1
- Prozentzahl: 1% => 0,01
- Prozentzahl: 0% => 0,00
Auch hier ist es eigentlich ganz simpel: Die Prozentangabe durch 100 dividieren ergibt die Dezimalzahl. Prozent heisst nichts anderes als Hundertstel.
Prozentsätze fürs Kopfrechnen
| Bequeme Prozentsätze | 1% | 5% | 10% | 12.5% | 20% | 25% | 33.333 % | 50% | 66.667 % | 75% |
| Bruchdarstellung | 1/100 | 1/20 | 1/10 | 1/8 | 1/5 | 1/4 | 1/3 | 1/2 | 2/3 | 3/4 |
| Dezimaldarstellung | 0.01 | 0.05 | 0.1 | 0.125 | 0.2 | 0.25 | 0.333 | 0.5 | 0.667 | 0.75 |
Prozentrechnung: Grundwert, Prozentsatz und Prozentwert
Prozentangaben verwendet man in der Prozentrechnung, um Anteile an etwas Ganzem anzugeben. Wir sehen uns dazu gleich einige Beispiele an. Davor ist es jedoch sinnvoll die Gleichungen und Begriffe zur Prozentrechnung einmal kurz zu behandeln. Zunächst einmal haben wir:
- „G“ für den Grundwert (das Ganze)
- „p%“ für den Prozentsatz (der Anteil in Prozent).
- „W“ für den Prozentwert (der Bruchteil des Ganzen)
Einführungs- und Demonstrationsbeispiel
Gegeben sind 5kg Mehl.
20% davon schenken wir dem Nachbar.
| Erklärung | Beispiel |
| Der Grundwert ist das Ganze und ist immer 100%. | Z.B. seien 5kg Mehl 100%. |
| Der Prozentsatz ist der Anteil der 100% in Prozent angegeben | Also z.B. 20% des gesamten Mehls (Grundwert). Also 0.2 * 5kg = 1kg |
| Der Prozentwert ist der Bruchteil des Ganzen, also der Bruchteil Grundwertes. | 20% ist also 1kg Mehl. |
Drei mögliche Aufgabenstellungen
Je nach Aufgabenstellung ist gesucht:
- der Grundwert
- der Prozentwert
- der Prozentsatz
Alle drei Typen werden gleich ausführlich besprochen.
Um diese gesuchten Angaben zu berechnen, setzt die in einer Aufgabe verfügbaren Informationen in diese Gleichungen ein:
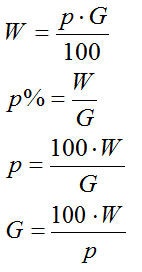
1. Typ: Prozentwert gesucht
Es wurde ein Bus gemietet um eine Gruppe von 50 Personen ins Theater zu fahren. Von diesen 50 Personen haben jedoch erst 30% die Fahrt bezahlt. Wie viele Personen haben bereits bezahlt?
Gegeben:
Gruppe von 50 Personen (100%)
30% haben bezahlt.
Gesucht:
Wie viel sind 30% der Gruppe?
Gesetze:
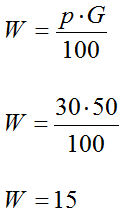
Lösung: Dem Text entnehmen wir, dass G = 50 Personen sein muss. Der Prozentsatz ergibt sich zu p% = 30% und damit ist die Prozentzahl p = 30. Den Prozentwert W suchen wir. Mit diesen Angaben gehen wir in die Gleichung und erhalten den Prozentwert W = 15 Personen. Es haben somit erst 15 Personen die Fahrt bezahlt.
2. Typ: Prozentsatz gesucht
Beispiel: Ein Autohändler kauft ein Auto für 10’000 Euro. Zwei Monate später schafft er es dieses für 12’000 Euro wieder zu verkaufen. Wie viel Prozent Gewinn hat er damit erwirtschaftet?
Gegeben
Grundwert (100%) = 10’000 €
Prozentwert = 12’000 – 10’000 €
Gesucht
Prozentsatz (in %)
Gesetze:
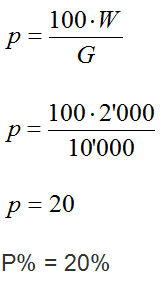
Lösung: Wir entnehmen der Aufgabenstellung, dass G = 10’000 Euro ist. Ausserdem können wir W = 12’000 Euro – 10’000 Euro = 2’000 Euro ermitteln. Der Händler verkauft den Wagen somit 2’000 Euro teurer als er ihn eingekauft hat. Mit diesen Angaben gehen wir in die Gleichung und ermitteln die Prozentzahl zu p = 20 und den Prozentsatz zu p% = 20%. Also hat der Händler 20% Gewinn erwirtschaftet.
3. Typ: Grundwert gesucht
Beispiel: In einer Schule sind 420 Mädchen eingeschrieben. Dies sind 70% aller Schüler. Wie viele Schüler lernen in dieser Schule?
Gegeben:
Prozentwert = 420 Mädchen
Prozentsatz = 70%
Gesucht:
Grundwert
Gesetze:
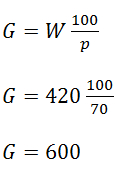
Lösung:
Die 420 Mädchen sind der Prozentwert W. Er entspricht einem Prozentsatz p% von 70% oder einem Anteil von 0.7. Der Prozentwert W kann direkt durch Anteil von 0.7 dividiert werden, und man erhält das Resultat. Wird der Prozentwert durch den Prozentsatz p% dividiert, muss er noch mit 100 multipliziert werden. Wir erhalten den Grundwert G = 600 Schüler.
Prozentuale Veränderungen
Verringert sich der Grundwert um einen bestimmten Prozentsatz, so spricht man von einem prozentualen Abschlag bzw. von einem verminderten Grundwert.
G – = G (100% – p%)
Vermehrt sich der Grundwert um einen bestimmten Prozentsatz, so spricht man von einem prozentualen Zuschlag bzw. einem vermehrten Grundwert.
G + = G (100% + p%)
Promillerechnung
Ein Promille vom Grundwert G ist ein Tausendstel von G.