Optimierung: Finden des Maximums

1. Optimierungsaufgabe

Aus einem festen rechteckigen Karton mit dem Abmessungen 50cm × 30cm ist eine Schachtel – ohne Deckel – herzustellen, indem man an allen vier Ecken gleich grosse Quadrate ausschneidet und den verbleibenden Rest zur Schachtel biegt. Welche Quadrate muss man ausschneiden, so dass die entstehende Schachtel das grösste Fassungsvermögen erhält?

Hier der Karton mit den Massen:

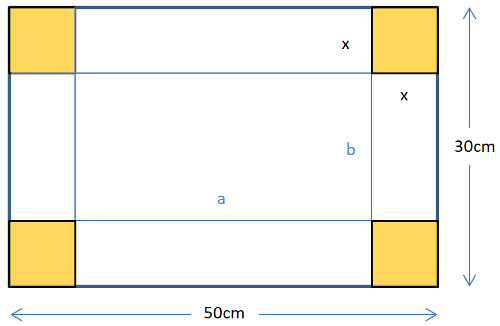
x ist die Höhe des Quaders (bzw. der Schachtel).

Je grösser x, desto kleiner die Grundfläche des Volumens.

Das Volumen berechnet sich als: V = a · b · x
a = 50cm – 2x
b = 30cm – 2x

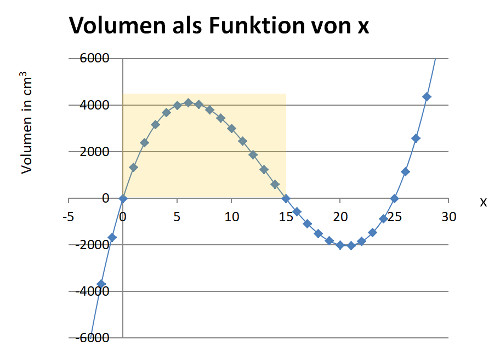
Wenn nun das Volumen als Funktion von x untersucht wird, erhalten wir eine parabolische Kurve.

Wertetabelle

x	y
0	0
1	1344
2	2392
3	3168
4	3696
5	4000
6	4104
7	4032
8	3808
9	3456
10	3000
11	2464
12	1872
13	1248
14	616
15	0

Wie man aus der Kurve sehen kann, ist im realen Bereich (positive Volumenwerte, farbig hinterlegt) das Maximum bei etwa 6, was in der folgenden Abbildung sichtbar ist.

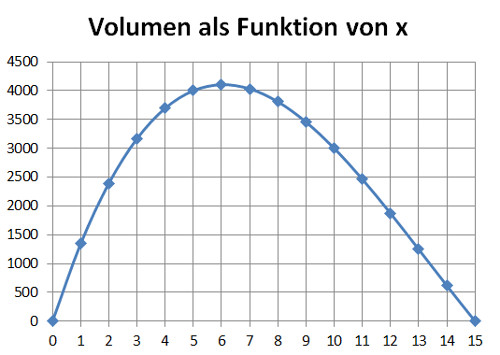
Das genaue Maximum der Kurve kann rechnerisch nur durch Ableitung ermittelt werden. In der Volksschule begnügen wir uns mit Annäherung.

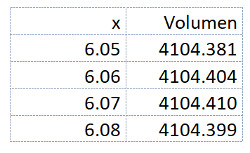
Da die Veränderung zwischen x = 6.06 und x = 6.07 verglichen mit x = 6.07 und 6.08 kleiner ist, suchen wir das Maximum unterhalb von x = 6.07.

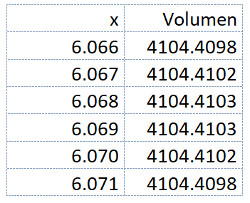
Ein annähernd genaues Resultat ist also x = 6.0685 cm. Dieses kann aber ohne grossen Aufwand noch genauer angenähert werden.

Die grösste Schachtel bezüglich Volumen erhalten wir also, wenn die Höhe x = 6.0685cm gewählt wird.

2. Optimierungsaufgabe

Es stehen mir 8m Zaun zur Verfügung, um ein Gehege für meine Kaninchen zu bauen. Es soll ein rechteckiges Gehege so platziert werden, dass es von zwei Seiten von Hauswand und Gartenmauer begrenzt wird. Wie lang müssen die Seiten x und y sein, dass das Gehege möglichst gross wird?

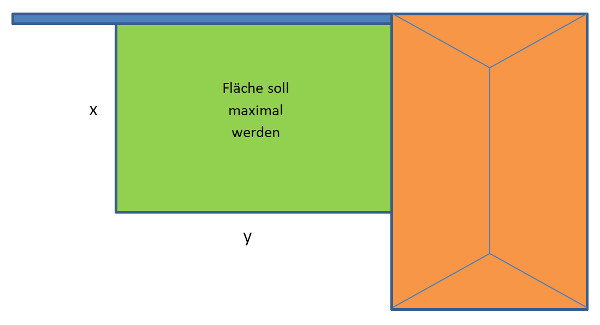
Wenn die vorhandenen 8m Zaun in ein x- und ein y-Stück aufgeteilt werden sollen, können wir das wie folgt schreiben:

x
y = 8m – x

Für die Fläche gilt dann:

A = x ( 8 – x)

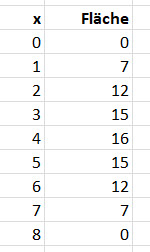
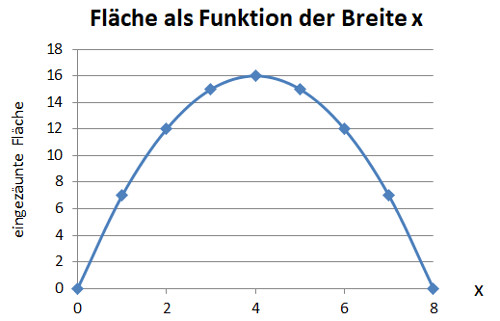
Wertetabelle

3. Optimierungsaufgabe

Aus einer Holzplatte in Form eines gleichschenkligen rechtwinkligen Dreiecks soll entsprechend der Abbildung ein möglichst grosses, rechteckiges Stück herausgesägt werden. Die Grundseite des Dreiecks ist 2m lang. Wie lang müssen die Seiten x und y sein?

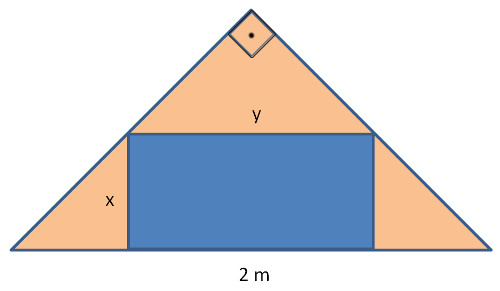
Es gilt: y = 2m – 2x

Die Rechtecksfläche ist also: A = x · y = x (2 – 2x) = 2x – 2x²

Wiederum wird die Rechtecksfläche als Funktion von x dargestellt:

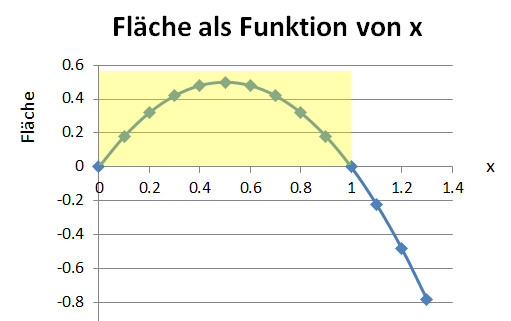
Der gelb hinterlegte Teil der Kurve (Parabel) ist positiv und somit einzig real. Da die Kurve symmetrisch ist, sehen wir, dass das Volumen dann maximal ist, wenn x genau 50cm.