Zwei Punkte definieren eine Gerade

Durch zwei Punkte kann nur eine ganz bestimmte Gerade gezeichnet werden. Eine Gerade im Koordinatensystem hat genau zwei Eigenschaften:

a: Steigung: a = h/x

b: Schnittpunkt mit der y-Achse (y-Achsenabschnitt)

Die Normalform (Hauptform) der Geradengleichung

Funktionen der Form y = ax + b nennt man lineare Funktionen.

Der Graph ist eine Gerade, welche durch den Punkt P(0|b) geht.
b ist der y-Achsenabschnitt
a ist die Steigung.

Eine Funktionsgleichung mit 2 Unbekannten muss zuerst von der allgemeinen Form in die Normalform gebracht werden:

Allgemeine Form einer linearen Funktionsgleichung

ux + vy + w = 0

Normalform einer linearen Funktionsgleichung

y = ax + b

Umwandlung von allgemeiner in Normalform:

ux + vy + w = 0   | Gleichung durch v dividieren und nach y auflösen
y + (u|v)x + (w|v) = 0
y = – (u|v)x – (w|v)

a = – (u|v)
b = – (w|v)

Beispiel:
4x + 2y – 8 = 0   | Ganze Gleichung durch 2 teilen
2x + y – 4 = 0     | Gleichung umstellen
y = – 2x + 4

Darstellung einer linearen Funktion im kartesischem Koordinatensystem

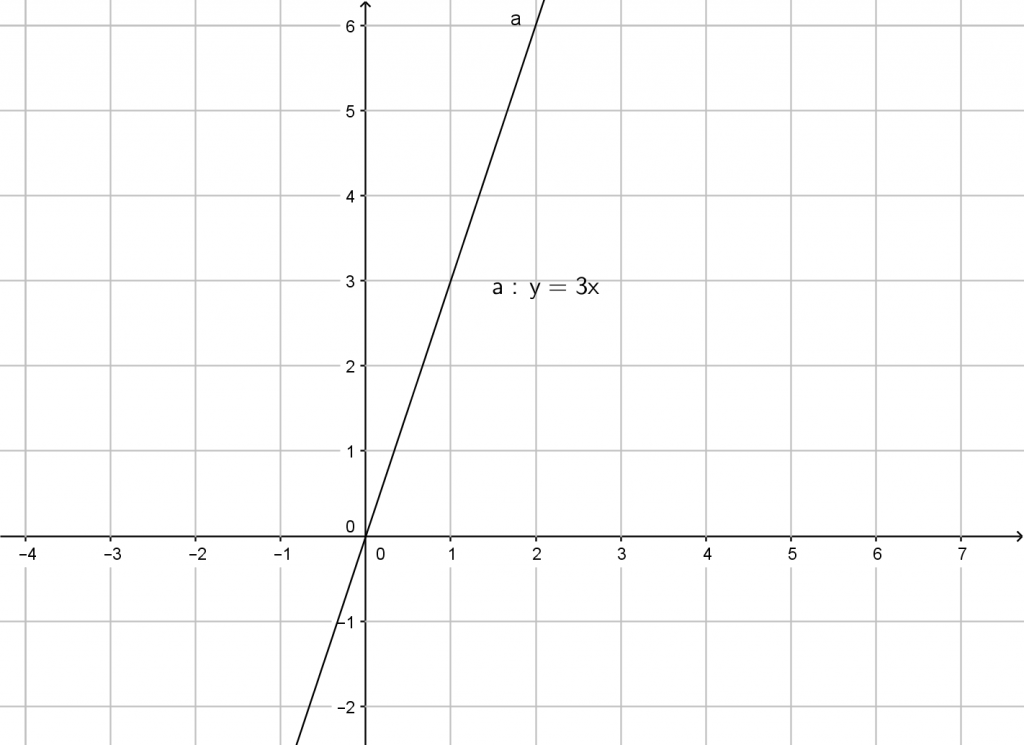
Zunächst brauchen wir eine Funktionsgleichung, wir nehmen als Beispiel y = 3x.
Dann stellen wir eine sogenannte Wertetabelle auf: Wir erstellen eine Tabelle mit einer x-Spalte und einer y-Spalte.

Dann tragen wir in die x-Zeile beliebige (für den angeschauten Bereich sinnvolle) Zahlen ein und rechnen diese mit Hilfe der Funktionsgleichung aus. x-Wert = 3, also y = 3⋅3 = 9.
Das machen wir mit allen anderen x-Werten auch und tragen die ermittelten y-Werte in die zweite Zeile der Tabelle ein.

y = 3x
x	y
-2 -1 0 1 2 3 4	-6 -3 0 3 6 9 12

Nun zeichnen wir alle ermittelten Punkte ins Koordinatensystem ein (für die Gerade reichen theoretisch zwei Punkte).
Zuletzt verbinden wir noch die Punkte und ziehen die Gerade, so entsteht der Graph.

Schnittpunkte mit den Koordinatenachsen

Wann schneiden Funktionsgraphen die y-Achse? Wenn x = 0
Wann schneiden Funktionsgraphen die x-Achse? Wenn y = 0

Verschiedene Fragestellungen und Rechen-Beispiele

Gegeben ist die Steigung und ein Punkt. Gesucht die Funktionsgleichung

Beispiel:
Gegeben
a = 2 und P (2 | 3)
y = ax + b
Wir setzen die Punktkoordinaten in die Funktionsgleichung ein
3 = 2 ⋅ 2 + b
Wir bestimmen den y-Achsenabschnitt und erhalten die Funktionsgleichung
b = –1
Lösung: y = 2x – 1

Gegeben ist der y-Achsenabschnitt und ein Punkt. Gesucht ist die Funktionsgleichung

Beispiel:
Gegeben:
b = 3 und P (5 | –7)
y = ax + b
Gegebenes einsetzen:
– 7 = a ⋅ 5 + 3
5a = 10
a = 2
Lösung: y = 2x + 3

Gegeben sind zwei Punkte A und B (mit Koordinaten)

Beispiel:
Gegeben: A (1 | 5) und P (4 | 2)
Ich zeichne die beiden Punkte in ein Koordinatensystem:

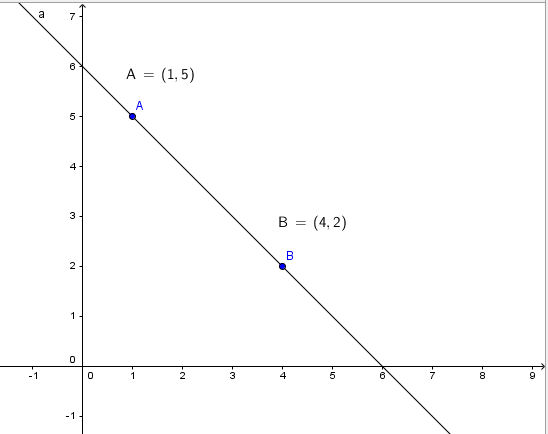
Die Steigung der Geraden berechnen wir, indem wir die Formel a = Δy / Δx anwenden.
Δy = y_a – y_b = 5 – 2 = 3
Δx = x_a – x_b = 1 – 4 = -3
a = Δy / Δx = -1
Den y-Achsenabschnitt berechnen wir, indem wir indem wir einen Punkt in die Funktionsgleichung mit der Steigung einsetzen:
y = –1⋅x + b
5 = –1⋅1 + b
b = 6
Lösung: y = – x + 6  (a = –1 und b = 6)

Gegeben die Funktionsgleichung und ein x-Wert. Gesucht ist der y-Wert

Beispiel
Gegeben:
y = 0.5x – 4
x = 8
x-Wert in die Funktionsgleichung einsetzen:
y = 0.5⋅8 – 4 = 0
Lösung: y = 0

Gegeben die Funktionsgleichung und ein y-Wert. Gesucht ist der x-Wert

Beispiel
Gegeben:
y = 5x – 2 und y = 10
Wir setzen wieder in die Funktionsgleichung ein:
10 = 4x – 2
4x = 12
x = 3
Lösung: der x-Wert ist x = 3