Theorie der Kunst des Zählens

Die Kombinatorik ist die Kunst des Zählens. Mit diesem Teilgebiet der Mathematik können wir die Zahl der möglichen Anordnungen oder Auswahlen von Objekten bestimmen.

Bestimmung der Zahl möglicher Anordnungen oder Auswahlen von
unterscheidbaren oder nicht unterscheidbaren Objekten
mit oder ohne Beachtung der Reihenfolge.

Entscheidungsbaum zur Kombinatorik

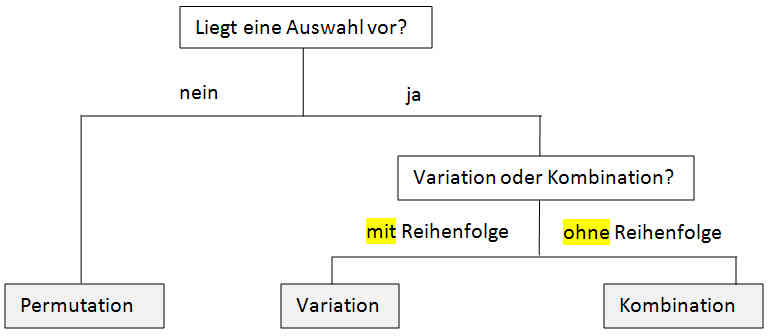
Permutation

Anzahl Möglichkeiten = n!

mit n: Anzahl Objekte

Typische Aufgaben sind die folgenden:

Ordne die vier Ziffern 1, 2, 3, 4 in allen möglichen Reihenfolgen. Wie viele gibt es?

1234 1243 1324 1342 1423 1432

2134 2143 2314 2341 2412 2421

3124 3142 3214 3241 3412 3421

4123 4132 4213 4231 4312 4321

Bilde aus den vier Buchstaben ROMA alle möglichen Reihenfolgen. Welche hat eine Bedeutung?

ROMA	ORMA	MROA	AROM
ROAM	ORAM	MRAO	ARMO
RMOA	OMRA	MORA	AORM
RMAO	OMAR	MOAR	AOMR
RAOM	OARM	MARO	AMRO
RAMO	OAMR	MAOR	AMOR

ROMA (Stadt Rom),
RAMO (dat.sing. von ramus = Zweig)
ORAM (acc.sing. von ora = Rand, Grenze)
MORA (Verzögerung, Rast)
MARO (Familienname des Dichters Publius Vergilius Maro)
AMOR (Gott der Liebe)
ARMO (1. Person Präs. Aktiv von armare: ich rüste auf)

Permutation mit einer Wiederholung

Die Anzahl der Permutationen von n Objekten, von denen k identisch und damit nicht unterscheidbar sind, berechnet sich zu

Beispiel: SAAL

Berechne die Anzahl der Anordnungen.

n = 4   Das Wort hat 4 Buchstaben
k = 2   Zwei der Buchstaben (AA) sind identisch

4! / 2! = 24 / 2 = 12 Möglichkeiten

AALS AASL ALAS ALSA ASAL ASLA
LAAS LASA LSAA SAAL SALA SLAA

Permutation mit mehreren Wiederholungen

Gibt es nicht nur eine, sondern s Gruppen, mit jeweils k₁,…,k_s identischen Objekten, so lautet die Formel

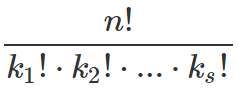
Beispiel: MISSISSIPPI

Auf wie viele Arten kann das Wort Mississippi angeordnet (permutiert) werden?

n = 11    es hat 11 Buchstaben
k1 = 4   Der Buchstabe I kommt 4 mal vor
k2 = 4   Der Buchstabe S kommt 4 mal vor
k3 = 2   Der Buchstabe P kommt 2 mal vor

Es gibt also 34’650 Möglichkeiten, das Wort anzuordnen.

Hier gibt es einen Permutations-Generator.

Variation

Eine Variation oder geordnete Stichprobe ist eine Auswahl von Objekten mit einer bestimmten Reihenfolge.

• Darf jedes Objekt nur einmal auftreten spricht man von einer Variation ohne Wiederholung.
• Können Objekte mehrfach ausgewählt werden, so spricht man von einer Variation mit Wiederholung. 

Variation ohne Wiederholung

Mögliche Anordnungen:

Beispiel: Ziehen von 3 Kugeln aus Urne mit 5 verschiedenen Kugeln

Wenn aus einer Urne mit fünf verschiedenen Kugeln dreimal ohne Zurücklegen gezogen wird, sind 5 ⋅ 4 ⋅ 3 = 60 verschiedene Auswahlen möglich.

Ohne Wiederholung heisst bei der Urne auch: Ohne Zurücklegen.

Variation mit Wiederholung

Mögliche Anordnungen:

n^k

Die Ermittlung der Anzahl möglicher Variationen ist eine Standardaufgabe der abzählenden Kombinatorik.

Beispiel: Ziehen von 3 Kugeln mit Zurücklegen aus Urne mit 5 verschiedenen Kugeln

Wenn aus einer Urne mit fünf verschiedenen Kugeln dreimal mit Zurücklegen gezogen wird, dann sind 5 ⋅ 5 ⋅ 5 = 5³ = 125 verschiedene Auswahlen möglich

Kombination

Eine Kombination oder ungeordnete Stichprobe ist eine Auswahl von Objekten ohne Reihenfolge.

Bei einer Kombination ohne Wiederholung werden k aus n Objekten ohne Beachtung der Reihenfolge ausgewählt, wobei jedes Objekt nur einmal ausgewählt werden kann.

Kombination ohne Wiederholung

In einer Urne befinden sich fünf verschiedenfarbige Kugeln. Es sollen drei Kugeln ohne Zurücklegen (= ohne Wiederholung) und unter Beachtung der Reihenfolge gezogen werden. Wie viele Möglichkeiten gibt es?

Kombination mit Wiederholung

 

Die Permutation ist eine Anordnung. Es werden alle Elemente der Grundmenge betrachtet.
Die Reihenfolge wird berücksichtigt.

Bei der Variation oder Kombination wird nur eine Auswahl (Stichprobe) der Grundmenge betrachtet.

Bei der Variation wird die Reihenfolge berücksichtigt.

Bei der Kombination wird die Reihenfolge nicht berücksichtigt.

Zurück zur Mathe-Seite