In der Geometrie bezeichnet geometrischer Ort (Mehrzahl: geometrische Örter) eine Menge von Punkten, die eine bestimmte, gegebene Eigenschaft haben. In der ebenen Geometrie ist dies in der Regel eine Kurve, wofür man auch das Wort Ortskurve oder Ortslinie verwendet.

Ein Punkt wird dadurch bestimmt, dass zwei Ortslinien angegeben werden, deren Schnittpunkt er bildet. Im klassischen Fall sind das zwei Geraden, zwei Kreise oder eine Gerade und ein Kreis.

Hier die fünf klassischen Ortslinien in der ebenen Geometrie:

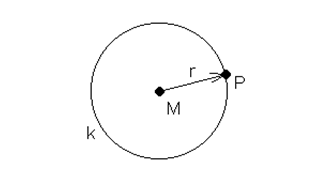	Die Ortslinie aller Punkte (der geometrische Ort aller Punkte), die von einem gegebenen Punkt M einen festen Abstand r haben, ist der Kreis k um M mit dem Radius r.
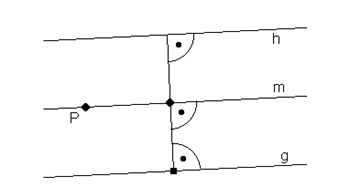	Die Ortslinie aller Punkte, die von einer gegebenen Geraden m einen festen Abstand d haben, ist das Paar von Parallelen g und h zu m im Abstand d.
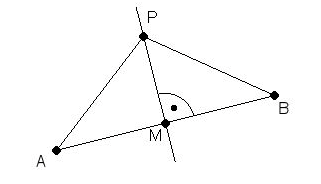	Die Ortslinie aller Punkte, die von zwei gegebenen Punkten A und B den gleichen Abstand haben, ist die Mittelsenkrechte über der Strecke AB.
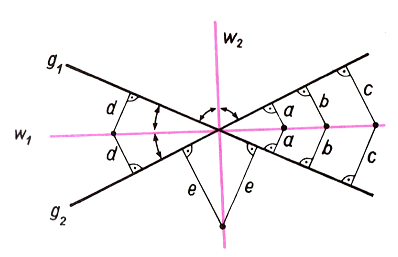	Die Ortslinie aller Punkte, die von zwei gegebenen sich schneidenden Geraden g1 und g2 den gleichen Abstand haben, ist das Paar von Winkelhalbierenden zu g und h.
	Die Ortslinie aller Punkte, die von zwei gegebenen parallelen Geraden g und h den gleichen Abstand haben, ist die Mittelparallele m zu g und h.

Übungen zu den geometrischen Örtern

Konstruiere alle Punkte P und gib die Lösungszahl an. Die Lösungszahl ist die Anzahl Lösungspunkte.

Aufgabe 1