Der Dreisatz ist eine der Grundaufgabe, die man auf jeden Fall in der Schule üben muss. Daher wollen wir eine Methode darstellen, um immer ans Ziel zu kommen.
Jeder Dreisatz beginnt mit einem Wertepaar das zusammengehört:
400 Gramm Emmentaler kostet 7.50 €.
Danach folgt die Frage nach einem neuen Wertepaar:
Wie viel kostet 750 Gramm?
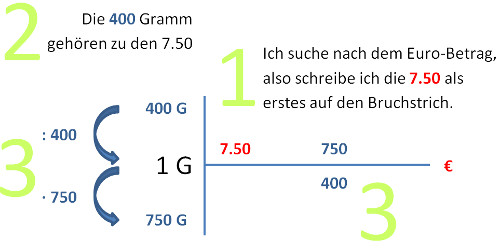
Methode, Dreisätze zu lösen
- ich suche nach dem Preis, also schreibe ich den gegebenen Preis auf den Bruchstrich.
- Ich schreibe das, was zu diesem Preis gehört, oben links neben den Balken.
- Anpassung an die neuen Zahlen durch Division und Multiplikation.
Dreisätze beruhen auf Proportionen
Dreisätze beruhen immer auf Proportionen. Es gibt zwei grundsätzliche Typen beim Dreisatz:
- direkte: Mehr Käse kostet mehr Geld, weniger kostet weniger.
- indirekte: Mehr Arbeiter brauchen weniger Zeit, weniger Arbeiter haben länger.
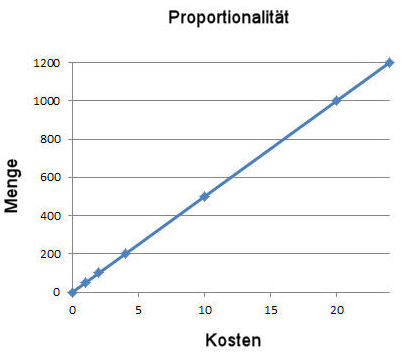
Erstes Beispiel: direkte Proportionalität
Ein Kilogramm Käse koste 20 Fr. Wie viel kosten 200 Gramm?
Mehr Käse kostet mehr, weniger Käse kostet weniger. Die Beziehung zwischen Käse und Preis ist proportional.
Merke: bei der direkten Proportionalität gilt:
Je mehr, desto mehr
je weniger, desto weniger
Wie rechne ich?
Gegeben 1 kg = 20 Fr.
Gesucht: 200 Gramm
Drei Sätze:
1000g kosten 20 Fr.
1 g Käse kostet tausendmal weniger: 20 : 1000
200g kosten 200-Mal mehr: 20 : 1000 * 200 = 4 Fr.
Darstellung mit dem Haken
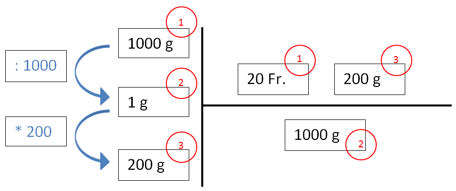
Vorgehen:
1. 1000 Gramm kosten 20 Franken. Da wir nach Franken suchen schreiben wir die 20 Fr. auf den Bruchstrich.
2. Der Schritt zu einer Mengeneinheit 1 Gramm: Unter den Bruchstrich schreiben wir 1000 Gramm
3. Von 1 Gramm zu 200 Gramm ist 200-mal mehr. 200 g auf den Bruchstrich schreiben.
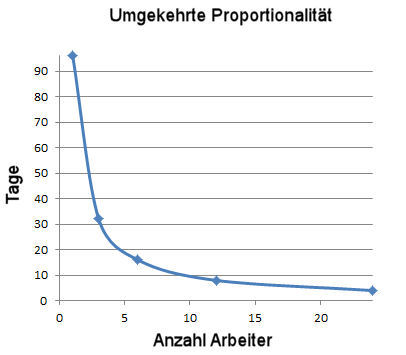
Zweites Beispiel: Indirekte oder umgekehrte Proportionalität
6 Arbeiter streichen die Zimmer eines Hauses in 8 Tagen. Wie lange brauchen für die selbe Arbeit 4 Arbeiter?
Mehr Arbeiter erledigen die Arbeit schneller, weniger brauchen dafür länger. Die Beziehung zwischen Anzahl Arbeiter und benötigter Zet ist umgekehrt proportional.
Merke: bei der indirekten Proportionalität gilt:
Je mehr, desto weniger
je weniger, desto mehr
Wie rechnen wir?
Drei Sätze:
6 Arbeiter benötigen 8 Tage
1 Arbeiter benötigt 6-mal länger: 8 Tage * 6 = 48 Tage
4 Arbeiter benötigen 4-mal weniger lang: 8T * 6 : 4 = 12 Tage
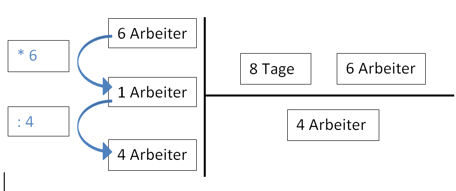
Erklärung
8 Tage kommt auf den Bruchstrich, denn wir wollen ja die Zeit in Tagen finden. Zu den 8 Tagen Arbeit gehören die 6 Arbeiter. Wenn nun nur 1 Arbeiter die Zimmer streicht, hat er 6 Mal länger: ein Faktor 6 kommt auf den Bruchstrich. 4 Arbeiter erledigen die Arbeit 4 Mal schneller, d.h. die Arbeitszeit verkürzt sich um 4. Die 4 kommt also in den Nenner als Divisor.
Übungen mit Lösungen
- 100 Gramm Tilsiter-Käse kosten 4.70 Fr. Wie viel kosten 180 Gramm?
- Für einen Zimmeranstrich kaufe ich Farbe. 5 Liter reichen für 30 Quadratmeter. Wie viel Liter muss ich für 75 Quadratmeter kaufen?
- Drei Arbeiter sind für einen Umbau aufgeboten. Sie brauchen für den Auftrag 4 Tage. Nun wird ein Arbeiter krank. Wie lange geht es nun?
- Ein Zwischenhändler kauft 8.5 Tonnen Salat für den Weiterverkauf. Er könnte dafür Fr. 5000 durch den Verkauf an Endhändler bekommen. Nun sind aber 700 Kilo verdorben. Wie viel kann er also noch bekommen?
- Für ein Bürogebäude muss ein Aushub erfolgen. 4 Lastwagen könnten dieses Aushubmaterial in 5 Tagen wegfahren. Nun aber soll es schneller gehen. Wie viele Lastwagen sind nötig, dass man das Material in 1 Tag wegschaffen kann?
- 14 Arbeiter kosten einen Dachdeckerbetrieb pro Halbjahr 410’000 Franken. Im zweiten Halbjahr gibt es mehr Aufträge und der Betrieb kann insgesamt 735’000 Franken für die Löhne der Dachdecker einsetzen. Wie viele Arbeiter kann er dazu noch einstellen?
- 7 Paletten Ziegel wurden geliefert. Dafür musste 1’827 Franken bezahlt werden. Nun sind aber 13 Paletten nötig. Wie viel muss zusätzlich bezahlt werden?
Lösungen
- 8.45 Franken (gerundet von 8.46)
- 12.5 Liter Farbe
- 6 Tage
- 4588.25 Franken (4588.2353)
- 20 Lastwagen
- 25 Arbeiter insgesamt (genau 25.09756). Also 11 Arbeiter mehr.
- Insgesamt 3393 Fr. Also zusätzlich 1566 Franken.