Brüche sind für viele ein schwieriges Thema. Dem wollen wir abhelfen!
Nach klaren Begriffserklärungen wollen wir zeigen, wie man einen Bruch kürzt oder erweitert. Weiter lernen wir, wie Brüche addiert oder subtrahiert werden.
Am Schluss gibt es noch Übungsaufgaben mit Lösungen!
Definition: Bruch
Der Bruchstrich beim Bruchrechnen ist ein Geteilt-Zeichen. Es gilt:
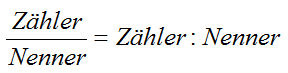
Die Zahl auf dem Bruchstrich nennt man den Zähler, die Zahl unter dem Bruchstrich ist der Nenner.
Kürzen und erweitern
Kürzen eines Bruches
Kann der Zähler und der Nenner durch die gleiche Zahl dividiert werden, so kann man ihn kürzen. Dann hat der Bruch im Zähler und im Nenner gleiche Faktoren.
Hat ein Bruch im Zähler und Nenner gleiche Faktoren, so können diese gekürzt werden:

Da der Faktor 2 und der Faktor 5 sowohl im Zähler als auch im Nenner auftaucht, können jeweils Zähler und Nenner durch diese Faktoren gekürzt werden. Der oben stehende Bruch kann also sowohl mit 2 wie auch mit 5 gekürzt werden.
Merke fürs Kürzen: Zähler und Nenner durch die gleiche Zahl dividieren.
Kürzen durch Zerlegung in Primfaktoren
Brüche können auch in Primfaktoren zerlegt werden. Gleiche Primfaktoren im Zähler und Nenner lassen sich dann direkt kürzen:
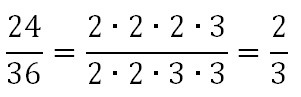
Gleiche Primfaktoren im Zähler und im Nenner können gekürzt werden.
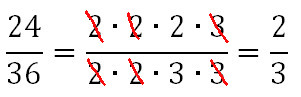
Hier noch ein komplizierteres Beispiel:
![]()
Wieder können gleiche Primfaktoren gekürzt werden:
![]()
Erweitern eines Bruches
Beim Kürzen steht zwischen den Ausdrücken ein Gleichheitszeichen. Somit gilt die Regel des Kürzens auch „rückwärts“. Brüche können also im Zähler und Nenner gleichzeitig mit beliebigen Faktoren (Zahlen) multipliziert werden. Dieses Vorgehen nennt man Erweitern des Bruches:
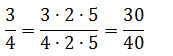
Merke fürs Erweitern: Zähler und Nenner mit der gleichen Zahl multiplizieren.
Multiplizieren Brüchen
Zwei Brüche werden multipliziert, indem man den Zähler des ersten mit dem Zähler des zweiten Bruches multipliziert und den Nenner des ersten mit dem Nenner des zweiten Bruches multipliziert.
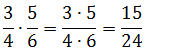
Merke: Zähler mal Zähler, Nenner mal Nenner
Dividieren von Brüchen
Ein Bruch wird durch einen zweiten Bruch dividiert (geteilt), indem wir vom zweiten den Kehrwert nehmen und die Brüche dann multiplizieren. Man erhält den Kehrwert eines Bruches indem man den Zähler und den Nenner vertauscht. Der Kehrwert von 7/5 ist 5/7
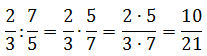
Merke: Bilde den Kehrwert des Divisors. Dann Zähler mal Zähler und Nenner mal Nenner
Auch wenn Brüche dividiert werden, kann natürlich das „Geteilt-Zeichen“ durch einen Bruchstrich ersetzt werden. Man erhält dann einen Doppelbruch.
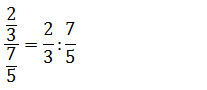
Addition und Subtraktion von Brüchen
Merke: Wenn Brüche gleichnamig sind, dann können wir einfach die Zähler addieren:
![]()
Wenn Brüche nicht gleichnamig, sondern ungleichnamig sind (also verschiedene Nenner haben), und man sie addieren will
![]()
… müssen sie zunächst auf den Hauptnenner, einfach gesagt einen gleichen Nenner gebracht werden. Man nennt dies „gleichnamig machen“.
Merke: ungleichnamige Brüche müssen zuerst gleichnamig gemacht werden!
![]()
Wir finden den gleichen Nenner, indem wir die beiden Nenner multiplizieren. Somit erweitern wir den ersten Bruch mit 5 und den zweiten Bruch mit 4. Hauptnenner ist hier 20.
Wenn die Brüche gleichnamig sind, lassen sich die Zähler einfach addieren.
Ein weiteres Beispiel:
![]()
Beim ersten Bruch ist der erste Nenner 3 und der zweite Nenner 5. Die Brüche können erst addiert werden, wenn bei beiden Brüchen die gleiche Zahl im Nenner steht, wenn sie also gleichnamig sind. Zuerst müssen sie gleichnamig gemacht werden, was durch Erweitern erreicht wird. Der erste Bruch kann mit dem Nenner des zweiten und der zweite Bruch mit dem Nenner des ersten erweitert werden.
Zwischenbemerkung:
Den Hauptnenner finden wir, indem wir das kgV berechnen.
Wenn mehr als zwei Brüche addiert oder subtrahiert werden sollen, so muss jeder Bruch mit den Nennern aller anderen Brüche erweitert werden. Z.B.:
![]()
![]()
Brüche mit Variablen
Wenn die Nenner gemeinsame Faktoren enthalten, kann man sich allerdings die Arbeit leichter machen. Dies wird anhand des nachfolgenden Beispiels gezeigt:
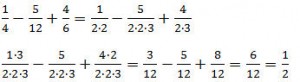
Hier reicht es, den ersten Bruch mit 3 und den dritten Bruch mit 2 zu erweitern, denn dann haben alle Brüche den gleichen Nenner.
Die Nenner brauchen also zum Addieren oder Subtrahieren nur auf das kleinste gemeinsame Vielfache gebracht zu werden.
Auch die Addition von Brüchen lässt sich „umdrehen“. Ein Bruch kann z.B. folgendermassen in mehrere Brüche aufgespalten werden:
![]()
oder auch
![]()
Es sei angemerkt, dass derartige Aufspaltungen nur mit dem Zähler (das was oben steht) und keinesfalls mit dem Nenner (das was unten steht) durchgeführt werden dürfen.
Unechte Brüche
Brüche, deren Wert grösser als 1 ist, schreibt man auch als gemischte Zahl. Z.B. schreibt man:
![]()
Den rechten Ausdruck nennt man eine gemischte Zahl. Es handelt sich um eine abkürzende Schreibweise, bei der das Pluszeichen weggelassen wird. Es gilt:
![]()
Wenn im Zähler oder Nenner Summen oder Differenzen stehen und gekürzt werden soll, so ist zu beachten, dass aus jedem Term gekürzt wird, das heisst, dass zuerst faktorisiert werden muss:
![]()
Abschliessend sei angeführt, dass ein Quotient genau dann Null ist, wenn der Zähler Null und der Nenner gleichzeitig ungleich Null ist. Folgendes Beispiel:
![]()
Nun wird der Zähler gleich Null gesetzt:
x – 2 = 0
x = 2
Wenn also x = 2 ist, dann ist der Wert des Quotienten gleich Null.
Beachte auch, dass bei x = – 2 der Wert des Quotienten nicht definiert ist, weil der Nenner eines Bruches nicht Null sein darf.
Übungen mit Lösungen


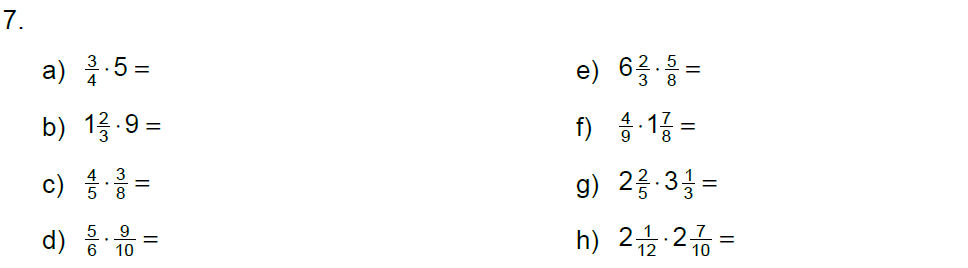
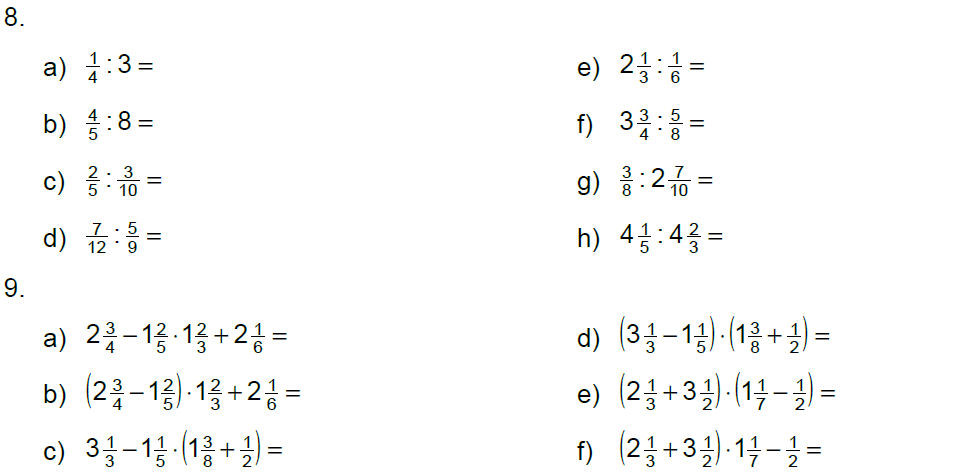
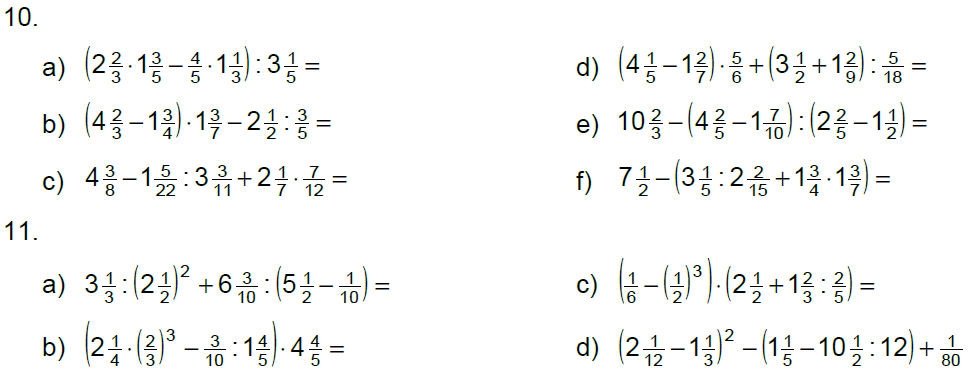
Lösungen
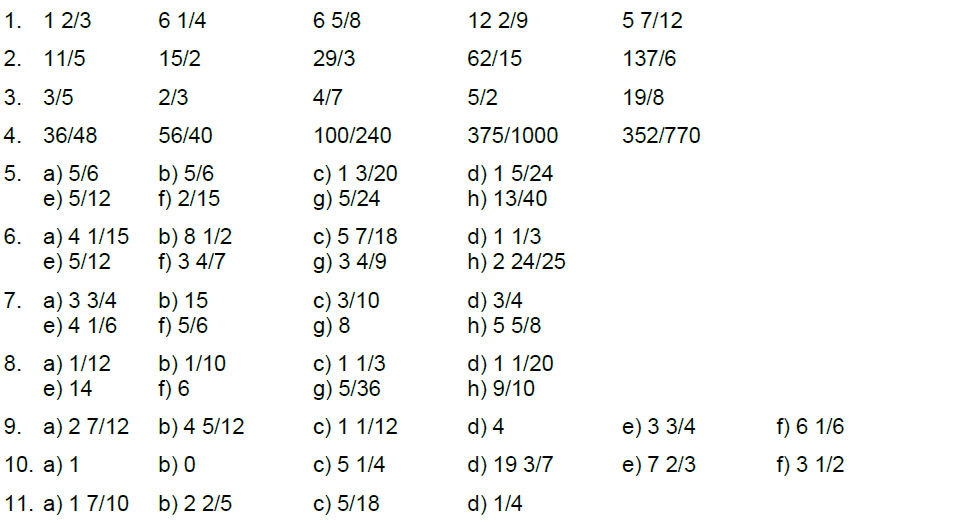
Verwandte Themen