Gauss – Zahlen addieren
Es war einmal an einer deutschen Schule, dass ein junger Schüler namens Carl Friedrich im Mathematikunterricht Unfug trieb. Sein Mathelehrer bekam dies mit und erteilte ihm eine Strafe. Jedoch nicht, wie es damals üblich war, eine Prügelstrafe, sondern eine «Mathestrafe».
Damit Carl Friedrich ruhig ist, wurde ihm aufgetragen die Zahlen von eins bis hundert zusammenzuzählen.
Die meisten Schüler würden fleissig anfangen zu addieren und eine Zeitlang beschäftigt sein. Der junge Carl Friedrich hingegen meldete sich nach wenigen Minuten. Der Lehrer wunderte sich über die Wortmeldung, da er ja soeben den Knaben beschäftigt hatte. Umso erstaunter war er, als Carl Friedrich gesagt hat, dass er die Aufgabe fertig habe und sogar das richtige Ergebnis sagen konnte.
Was hat Gauss gemacht?
Er hat Zahlen vom Anfang mit Zahlen vom Schluss addiert (siehe Tabelle unten)
| 1 | 2 | 3 | 4 | 5 | … | 97 | 98 | 99 | 100 |
| + | + | + | + | + | + | + | + | + | |
| 100 | 99 | 98 | 97 | 96 | 4 | 3 | 2 | 1 | |
| = | = | = | = | = | = | = | = | = | |
| 101 | 101 | 101 | 101 | 101 | 101 | 101 | 101 | 101 |
Danach hat er alle Summen der 100 Zahlen zusammengezählt: 100 x 101 = 10100. Das aber ergibt gerade das Doppelte der Lösung, da die Zahlen ja zweimal zusammengezählt worden sind.
Die Lösung von Gauss war also: 5050.
Die Addition von Zahlenreihen kann auch allgemein angewendet werden:
Die Formel lautet:
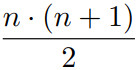
Angewendet auf die Zahlen von 1 bis 100 ergibt das 100 • (100 + 1) / 2 = 5050.