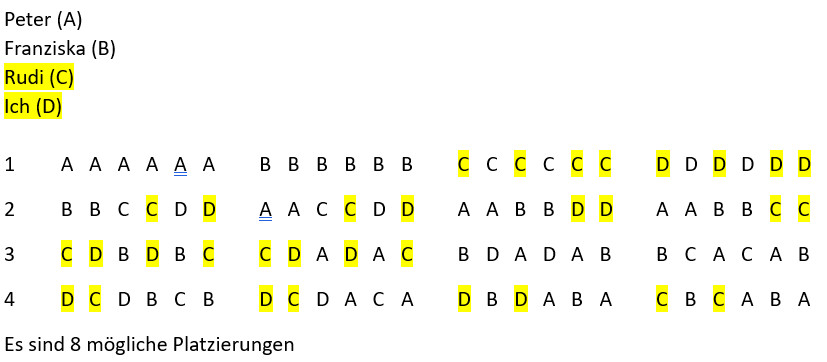
Auf wie viele Arten können wir Gäste an einem Tisch platzieren?
Auftrag 1:
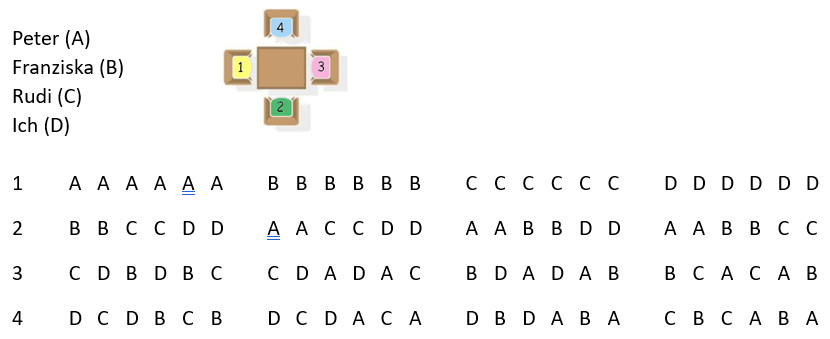
Ich lade drei Freunde ein: Peter, Franziska und Rudi. Die vier Plätze an meinem Tisch sind ganz unterschiedlich:
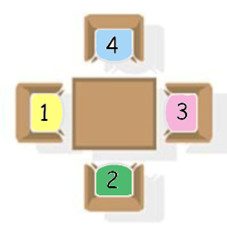
- Vom Platz 1 aus sieht man die Türe
- Vom Platz 2 aus sieht man durch das Fenster auf den Garten.
- Vom Platz 3 aus sieht man durch das Fenster auf die Strasse.
- Vom Platz 4 sieht man nur an die Zimmerwand.
Finde nun heraus, auf wie viele Arten du dich und die Gäste platzieren kannst. Überlege dir zuerst einmal, wie du am besten die Sitzordnungen darstellen kannst, so dass du den Überblick behältst.
Auftrag 2:
Nun lasst uns die Sache etwas komplizierter machen: Wie viele Sitzmöglichkeiten gibt es noch, wenn ich keinesfalls neben Rudi sitzen will?
Lösung Auftrag 1:
Was sich immer ändert, sind die Personen an den Plätzen. Zur Vereinfachung sagen wir:
- A ist Peter
- B ist Franziska
- C ist Rudi
- D bin ich
Für mich ist die folgende Darstellung übersichtlich. Vielleicht aber findest du noch eine bessere heraus. Machen wir uns die Sache einfacher: Lassen wir zuerst einmal Peter immer an Platz 1 sitzen. Wir sehen nun, dass es dann 6 verschiedene Sitzordnungen gibt.
| Platz 1 | A | A | A | A | A | A |
| Platz 2 | B | B | C | C | D | D |
| Platz 3 | C | D | B | D | B | C |
| Platz 4 | D | C | D | B | C | B |
Nun ist es nicht schwer, zu schliessen, dass dies für alle von uns gelten wird. Also: 4 x 6 Sitzordnungen, sprich 24 Sitzordnungen.
Lösung Auftrag 2:
Wenn ich nun auf keinen Fall neben Rudi sitzen will… Wir untersuchen in der obigen Darstellung, wann C und D nebeneinander liegen. Beachte, dass der Platz 1 auch neben Platz 4 ist.
| Platz 1 | A | A | A | A | A | A |
| Platz 2 | B | B | C | C | D | D |
| Platz 3 | C | D | B | D | B | C |
| Platz 4 | D | C | D | B | C | B |
Wir stellen fest, dass es von den 6 möglichen nur noch zwei genehme Sitzordnungen gibt. Also gibt es insgesamt 4 x 2 = 8