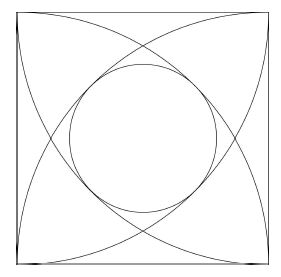
Berechne die Gesamtheit der Linien innerhalb des Quadrates, wenn eine Quadratseite 12cm misst.

Überlegungen zur Figur

Die vier Viertelkreislinien setzen sich zu einem Kreis mit Radius = 12 zusammen.
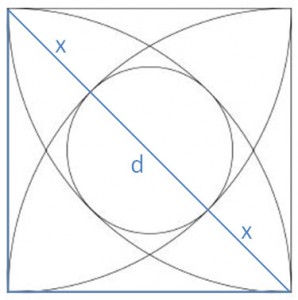
Um den Radius des inneren Kreises herauszufinden, müssen wir folgende Hilfslinien legen (siehe Abbildung).

Wenn wir von der Diagonale d den Radius 12cm subtrahieren, erhalten wir x. d – 2x wird nun zum Durchmesser des Innenkreises.

Berechnung der Linien

Länge der vier Viertelkreise L = 2 ⋅ 12cm ⋅ π = 75.398cm
Länge der Diagonale d = wurzel (12² + 12²) = 16.97cm
x = d – 12cm = 4.97cm
Radius des Innenkreises r = 0.5 ⋅ (d – 2x) = 3.51cm
Umfang des Innenkreises u = 22.08cm

Linien total L = 97.48cm

Zur nächsten Aufgabe

Zurück zur Auswahl der Kreisflächenberechnungen