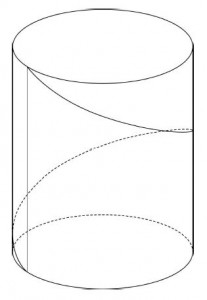
Um einen Zylinder mit der Höhe h = 10cm und dem Durchmesser von d = 4cm soll ein Faden so herumgelegt werden, dass von einem Punkt A auf dem oberen Rand zu einem Punkt B auf dem unteren Rand gelangen, dass er einmal den Zylinder umrundet. A und B liegen senkrecht übereinander.
Überlegungen
Mit Hilfe von einer Zeichnung machen wir uns die Verhältnisse anschaulich und klar:
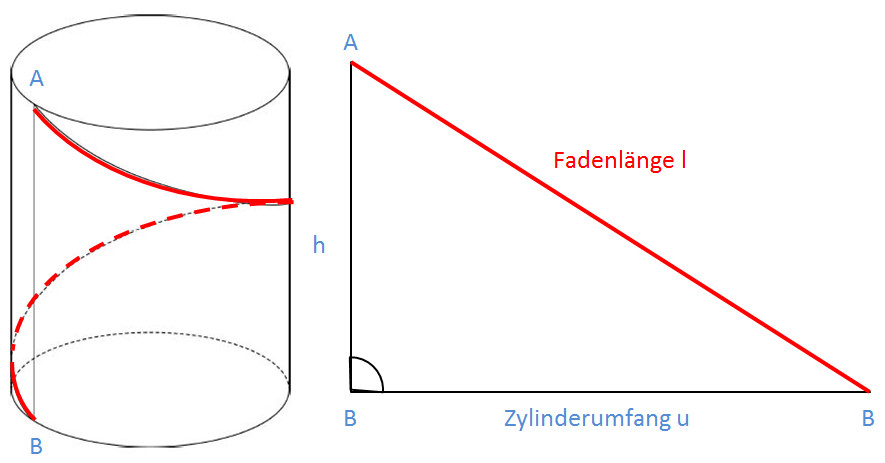
Die Abwicklung des Zylinders ergibt gerade ein Rechteck, der Faden liegt auf seiner Diagonale.
Das Rechteck hat die Masse h = 10 und u = Kreisumfang des Zylinderbodens.
Berechnung
Wir berechnen zuerst den Zylinderumfang u d ⋅ π = 4cm ⋅ π = 12.57cm
Mit Hilfe des Pythagoras können wir nun die Diagonale l berechnen:
Fadenlänge l = wurzel (h2 + u2) = 16.06 cm
Der Faden hat eine Länge von 16.06cm