Satz des Pythagoras
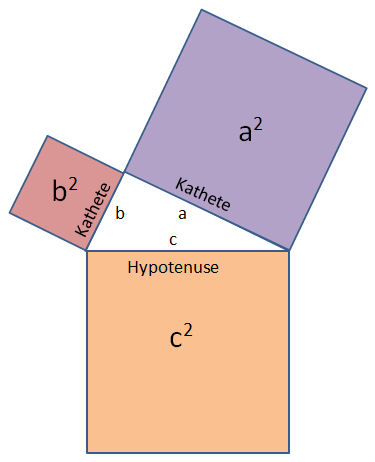
Im rechtwinkligen Dreieck ist der Flächeninhalt des Quadrates über der Hypotenuse gleich der Summe der Flächeninhalte der Quadrate über den Katheten.
c2 = a2 + b2
Es gibt für den Pythagoras mehr als 100 Beweise.
Einer davon ist der folgende:
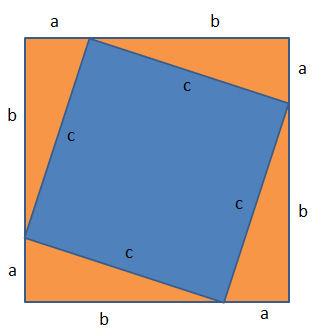
Die gesamte Quadratfläche beträgt (a + b)2
Sie ist zusammengesetzt aus dem Quadrat c2
und den vier rechtwinkligen Dreiecken ½ab zusammengesetzt.
Also:
(a + b)2 = c2 + 4⋅(½ab) = c2 + 2ab
a2 + 2ab + b2 = c2 + 2ab | – 2ab
a2 + b2 = c2 (was zu beweisen war / quot erat demonstrandum)
Anwendungen des Pythagoras
- Berechnung der dritten Seite eines rechtwinkligen Dreiecks, wenn die anderen zwei bekannt sind.
- Abstand zweier Punkte im Koordinatensystem
- Flächendiagonale und Raumdiagonale
- etc etc.
Berechnung der fehlenden Seite im rechtwinkligen Dreieck
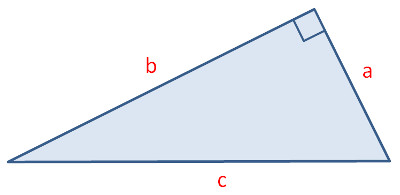
a2 + b2 = c2
Beispiel:
a = 3, b = 4, c = 5
32 + 42 = 52
Gegeben a und b
c2 = 9 + 16 = 25
c = 5
Gegeben a und c
25 = 9 + b2
b2 = 25 – 9 = 16
b = 4
Gegeben b und c
25 = a2 + 16
a2 = 25 – 16 = 9
a = 3
Allgemein
c2 = a2 + b2
a2 = c2 – b2
b2 = c2 – a2
Übungen
- Berechne die Hypothenuse (Seite c) eines rechtwinkligen Dreiecks, wenn
a = 10cm und b = 15cm - Berechne die Seite a eines rechtwinkligen Dreiecks, wenn b = 3cm und c = 5cm
- Berechne die Quadratseite, wenn der Durchmesser 5cm ist.
Lösungen
c = 18.028cm
a = 4cm
a = d/√2 = 3.536cm