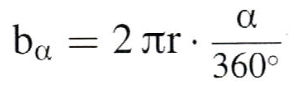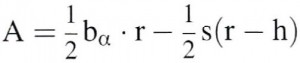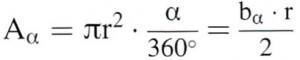Der Kreis ist sonderbar und alltäglich zugleich. Alltäglich, weil wir ihn in Sonne und Mond dauernd sehen. Sonderbar, weil er sich nicht simpel, sondern nur durch eine spezielle Kreiszahl π berechnen lässt. π ist gleich vielen Wurzelzahlen, der Eulerschen Zahl und anderen eine irrationale Zahl, d.h. sie hat unendlich viele nicht periodische Nachkommastellen.
π = 3.14159265359….
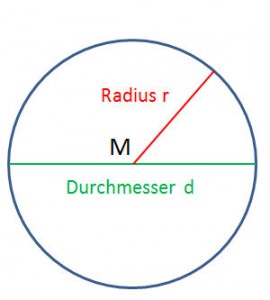
Was aber ist π? π gibt an, wie viel mal länger der Kreisumfang als sein Durchmesser ist.
KreisumfangUmfang des Kreises = Pi * Durchmesser u = r ⋅ π Der Kreisumfang ist Pi-mal grösser als der Durchmesser |
KreisflächeKreisfläche = Pi * Radius im Quadrat A = r2 ⋅ π Die Kreisfläche ist Pi-mal grösser als das Quadrat über dem Radius |
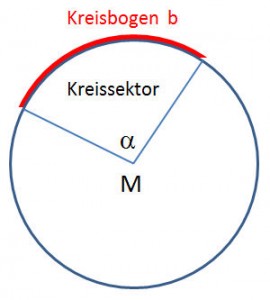
Kreisbogen und Kreissektor (Kreisausschnitt) |
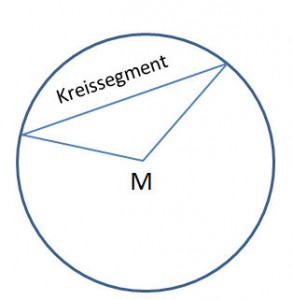
Kreissegment (Kreisabschnitt) |
| Kreisbogen und Kreissektor leiten sich von Kreisumfang resp. Kreisfläche ab:
|
Das Kreissegment leitet sich vom Kreissektor ab.
|
| Kreisbogen
Der Kreisbogen ist ein Teil des Kreisumfangs. Während der Kreisumfang für 360° gilt, ist der Kreisbogen nur über dem Winkel α. Die Formel des Kreisumfangs wird korrigiert durch den Faktor α/360°
|
Das Kreissegment (Kreisabschnitt) leitet sich rechnerisch vom Kreissektor (Kreisausschnitt) ab.
Dem Kreissektor wird das gleichschenklige Dreieck (mit den Radien als Schenkel) abgezogen. Zurück bleibt das Kreissegment.
|
| Kreissektor
Beim Kreissektor (Kreisausschnitt) wird die Kreisfläche durch den Faktor α/360° korrigiert.
|
Der Kreisring
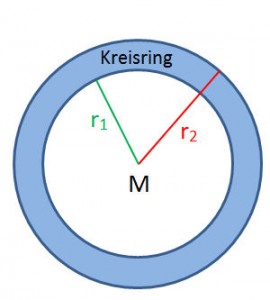
Die Berechnung des Kreisrings ist einfach: Berechne die Fläche des grösseren Kreises (r2) und ziehe davon die Fläche des kleineren Kreises (r1) ab.
Kreisring = π⋅r22 – π⋅r12