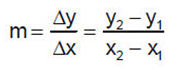Steigung auf Strassen

Die grösste Steigung einer Postauto-Strecke in Europa findet sich im Kiental, Kanton Bern, Schweiz. Angegeben ist sie mit 28%. Was heisst das?
Um Steigungen besser zu begreifen, wollen wir ein Steigungsdreieck zeichnen.
Definition der Steigung mit dem Steigungsdreieck
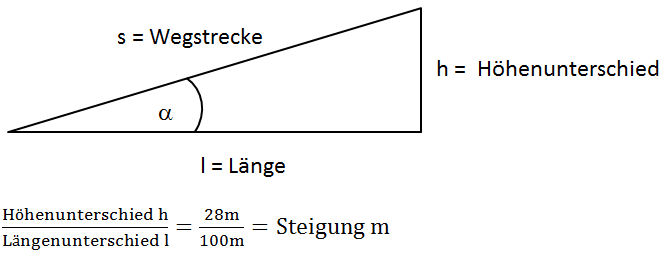
Die Steigung m ist definiert als Quotient von Höhenunterschied h und Längenunterschied l. Im Kiental ist dies an den steilsten Stellen 28m Höhenunterschied pro 100m.
Werden Steigungen in Prozent angegeben, heisst das, Anzahl Höhenmeter pro 100 Meter. Dann kann direkt die Steigung in Prozent abgelesen werden. Eine Steigung m aus beliebigen Werten von h und l muss daher noch mit 100 multipliziert werden, um die Steigung m in Prozent zu erhalten.
Merke: eine Steigung von 100% ist nicht senkrecht! Laut Definition ist es eine Höhendifferenz von 100m auf 100m Horizontaldifferenz.
Die senkrechte „Steigung“ hat den Wert m = unendlich.
Gefälle sind negative Steigungen, ihr m ist negativ.
Werte und Vorzeichen bei Steigungen

Aufgaben mit Lösungen
Die Höhendifferenz beträgt 180m. Auf der Karte misst die Strasse 4.5km. Wie gross ist die Neigung in Prozent?
Lösung: S.teigung = 4%
Die Orte A und B haben einen Höhenunterschied von 250m. Für Strassen wird eine maximale Steigung von 12% empfohlen. Wie lang wird also die Strasse zwischen diesen Orten mindestens sein?
Lösung: Länge der Strasse mindestens: 2083.33m
Die Jungfraubahn hat eine Länge von 9.34km. Von der kleinen Scheidegg bis zum Jungfraujoch auf 3’454 m.ü.M hat sie eine mittlere S.teigung von 14.9143%. Wie hoch liegt die kleine Scheidegg?
Lösung: Kleine Scheidegg: 2061 m.ü.M.
Der Öschibach fliesst auf einer Strecke von 2,18km von 1410 m.ü.M nach 1176 m.ü.M. Wie gross ist seine Steigung in Prozent?
Lösung: S.teigung = 10.73%
Gib die Steigung in % zwischen diesen Punkten des schweizerischen Karten-Koordinatennetzes an:
(616600/166100/400)
(614200/166100/1380)
Lösung: S.teigung = 40.83%
Steigung von Geraden im Koordinatensystem
Der Steigungsfaktor spielt eine wichtige Rolle bei den linearen Funktionen:
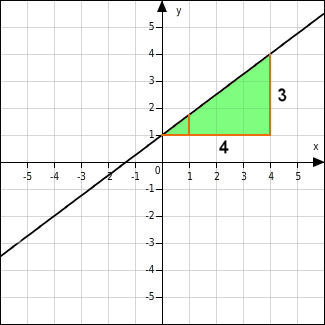
Im Koordinatensystem werden Steigungen (von Geraden, d.h. linearen Funktionen) genau gleich definiert:
Steigung m
m = Höhendifferenz / horizontaler Abstand
m = Δy : Δx
hier ist m = 3 : 4 = 0.75
m ist ohne Einheiten (die Streckeneinheiten kürzen sich.
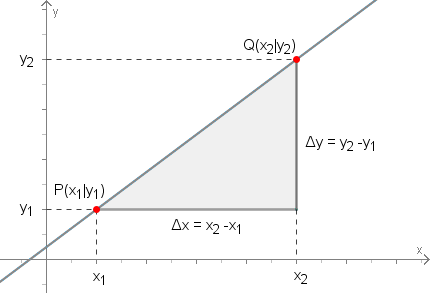
Allgemein im Koordinatensystem:
Zwei Punkte definieren genau eine Gerade (lineare Funktion), welche die Steigung m hat.
Aufgaben und Lösungen für Steigung im Koordinatensystem
Wie gross ist die Steigung zwischen den Punkten P1(2/2) und P2(0/4)?
Lösung: m = -1
Lösen von Steigungen mit dem Tangens (Winkelfunktion)
Wenn Steigungen mit Winkeln angegeben werden, können die restlichen Teile eines Steigungsdreiecks mit Hilfe von Winkelfunktionen gelöst werden:
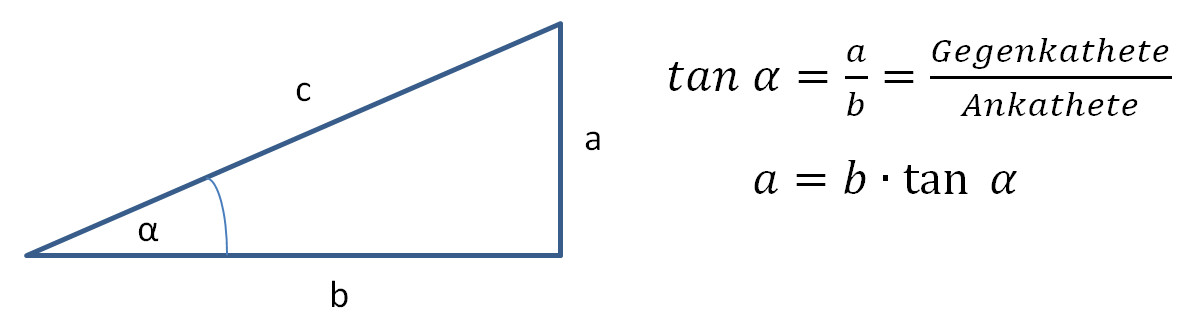
Entsprechend kann die Ankathete mit dem Kotangens und die Hypothenuse mit dem Sinus berechnet werden.
Aufgaben und Lösungen von Steigungsaufgaben mit Winkelfunktionen
Wie gross ist die Steigung bei einem 30° – Winkel?
tan 30° = a / b
b ist die Horizontaldistanz. Wir setzen sie gleich 100m.
Somit ist a (Höhendifferenz) = tan 30° * 100 = 57.74%
Die Neigung eines Garagendaches soll 15° betragen. Das Dach soll an der Hauswand die grösste Höhe haben. Die Breite der Garage ist 7m. Wenn die Garage innen mindestens 2.5m sein soll, wie hoch kommt das Dach an seiner höchsten Stelle?
Lösungsweg und Lösung:
tan α = Gegenkathete / Ankathete
tan 15° = x / 7m
x = tan 15° · 7m = 1.88m
Das Dach hat eine höchste Stelle von 8.88m
Verwandte Themen