Definition Dezimalbrüche

Der Dezimalbruch – auch Zehnerbruch genannt – ist aus 10-er-Stellen aufgebaut. Es kann aus einer Summe von Tausender, Hunderter, Zehner, Einer, Zehntel, Hundertstel etc. erklärt werden:

Tausender	Hunderter	Zehner	Einer	Komma	Zehntel	Hundertstel	Tausendstel
0	2	3	4	,	5	6	7
0 ⋅ 1000	2 ⋅ 100	3 ⋅ 10	4 ⋅ 1		5 ⋅ 0.1	6 ⋅ 0.01	7 ⋅ 0.001

Der Dezimalbruch 234,567 bedeutet damit:

0 ⋅ 1000 + 2 · 100 + 3 · 10 + 4 · 1 + 5 · (1/10) + 6 · (1/100)  + 7 · (1/1000)

Eigentlich ist ein Dezimalbruch ein Bruch, dessen Nenner eine Potenz von Zehn mit natürlichem Exponenten ist. Einfacher: Ein Bruch, in dessen Nenner 10, 100, 1000 usw. stehen kann.

Umwandeln eines Dezimalbruchs in einen Bruch

Abbrechende Dezimalbrüche werden als Bruch mit einer Zehnerpotenz im Nenner geschrieben und anschliessend gekürzt:

Umwandeln eines Bruchs in einen Dezimalbruch

Wir dividieren den Zähler durch den Nenner und erhalten den Dezimalbruch.

 

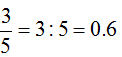
Addition und Subtraktion von Dezimalbrüchen

Schreibe Komma unter Komma, damit gleiche Stellenwerte untereinander stehen.

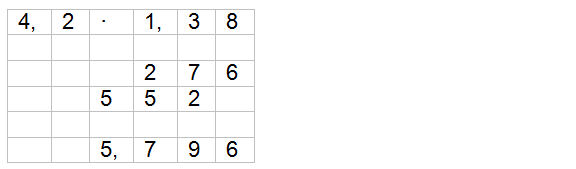
Multiplikation von Dezimalbrüchen

Das Produkt hat so viele Stellen, wie die beiden Faktoren zusammen aufweisen.

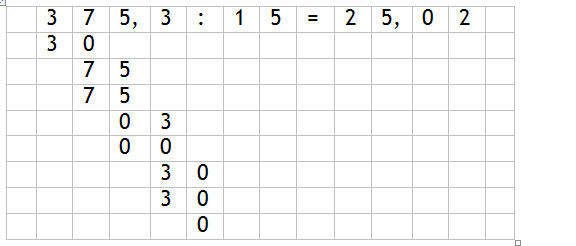
Division von Dezimalbrüchen

Erweitere so, dass im Divisor eine ganze Zahl entsteht.

37.53 : 1.5 = (37.53 · 10) : (1.5 · 10) = 375.3 : 15

Sobald das Komma im Dividend überschritten wird, setzt man das Komma im Quotient.

Unendliche Dezimalbrüche

Viele Divisionen führen in der Dezimalschreibweise zu unendlichen periodischen Dezimalbrüchen:

 

Verwandte Themen: Brüche