Ein Fadenpendel zeigt eine regelmässige Schwingung. Die Periodendauer T für ein Pendel berechnet sich mit der folgenden Formel:

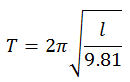
Je kürzer die Pendellänge l desto schneller schwingt das Pendel und desto kürzer ist die Periodendauer.

Amplitude, Periodendauer (Schwingungsdauer) und Frequenz vom Pendel

Wir betrachten noch einmal das Pendel. Versuchen wir einmal die Pendelbewegung in einem Schaubild (Diagramm) darzustellen.

Wenn ein Pendel schwingt, so findet eine ständige Auslenkung aus einem Zentrum statt. Die maximale Auslenkung wird als Amplitude bezeichnet.

y-t-Diagramm: Die Auslenkung im Laufe der Zeit festhalten.

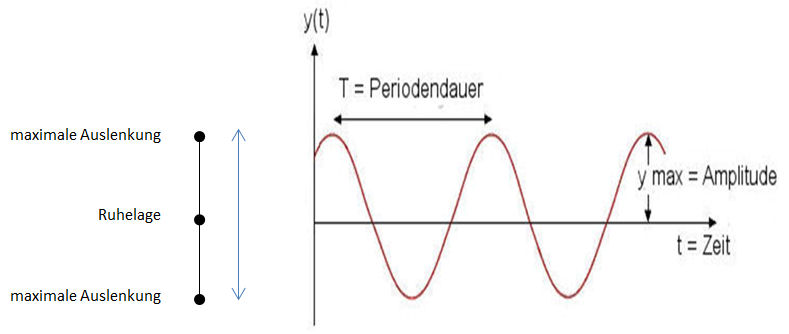
Die Pendelschwingungen sind regelmässig, unabhängig davon, ob das Pendel stark oder schwach pendelt. Wir haben dazu die Schwingungen pro Minute (Frequenz) gemessen.

Wenn eine Frequenz pro Sekunde angegeben wird, hat sie die Einheit Hertz (Hz).

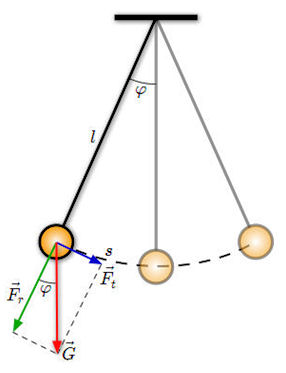
φ  Auslenkwinkel

l  Länge des Pendels

s  Auslenkung des Pendels: s = l ⋅ φ

G  Erdanziehungskraft G = m ⋅ g

g  Erdbeschleunigung = 9.81 m/s²

F_r  Kraftkomponente in Richtung Faden

F_t  tangentielle Kraftkomponente

m  Masse des Pendels

 

Frequenzen in Natur und Technik

1 m langes Pendel Herzschlag Tiefste für den Menschen hörbare Frequenz Flügel einer Hummel Sprechen Höchste von jungen Menschen hörbare Frequenz Ultraschall

0.5 Hz 0.7 Hz 16 Hz 200 Hz 100 – 1000 Hz 20000 Hz über 20000 Hz