Der Paul-Schatz-Würfel ist ein wunderbares Objekt. Schauen wir uns ihn etwas an:

Das innere Stück herausgelöst lässt sich in wundersamer Weise umstülpen:



Unser Ziel ist es, dieses Gebilde zu berechnen.
Berechnung
Der Würfelring besteht aus 6 Körpern, von denen je 2 spiegelsymmetrisch sind.
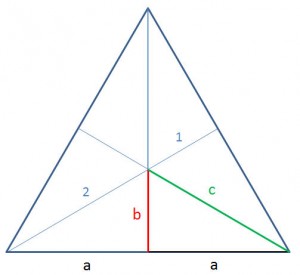
Die 6 Körper bilden in der obigen Abbildung (links und rechts) eine gleichseitiges Dreieck:
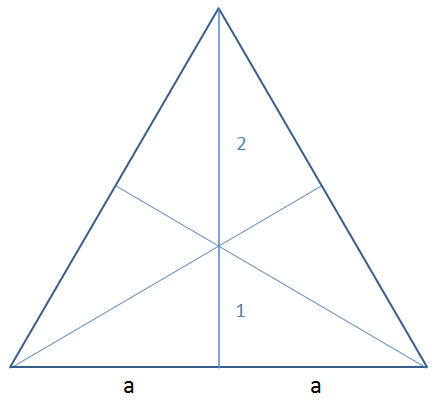
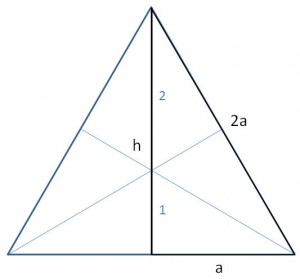
Es sei a die Würfelkante. Nun lassen sich alle anderen Stücke dieses gleichseitigen Dreiecks berechnen, indem wir die rechtwinklige Hälfte berechnen:
4a2 = h2 + a2
h2 = 3a2
h = wurzel (3a2) = a ⋅ wurzel (3)
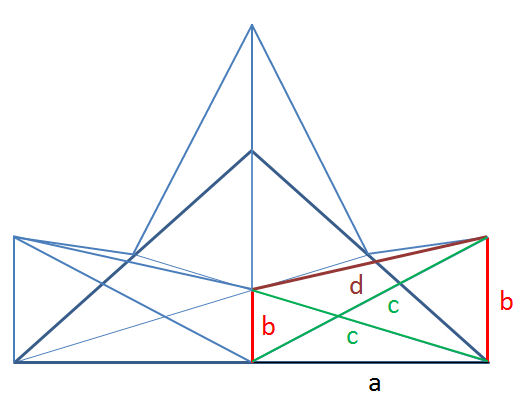
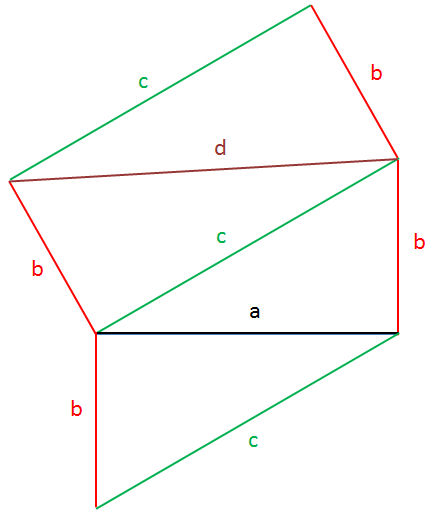
In der räumlichen Kantendarstellung ist einer dieser Drehkörper und die Kanten farbig herausgehoben:
b = 1/3 ⋅ h = a/3 ⋅ wurzel (3)
c = 2/3 ⋅ h = 2a/3 ⋅ wurzel (3)
d = wurzel (4/9 ⋅ h2 + 1/9 ⋅ h2) = wurzel (5/9⋅h2) = h/3⋅wurzel(5) = a⋅wurzel(3)/3⋅wurzel(5)
d = a ⋅ wurzel (15) / 3
Bastelbögen für die Herstellung eines solchen umstülpbaren Würfels samt Riegelkörper findet man im Internet bereitgestellt von Franz Zanek (www.fzk.at) Dabei empfiehlt es sich aber, die Einzelkörper auseinander zu schneiden und als „Scharniere“ Stoffreste zu verwenden. Papier ist zu steif und geht schnell kaputt!