Wie können wir die Kreiszahl Pi berechnen?
Was ist Pi?
Pi ist die Konstante, welche angibt, wie viel mal länger die Kreislinie als der Durchmesser ist. Also: Kreisumfang u = Durchmesser · π
Der Taschenrechner hat π gespeichert als 3.14159265359, also mit 11 Nachkommastellen.
Können wir diese Konstante π selber berechnen?
Idee: Annäherung der Kreislinie über Vielecke
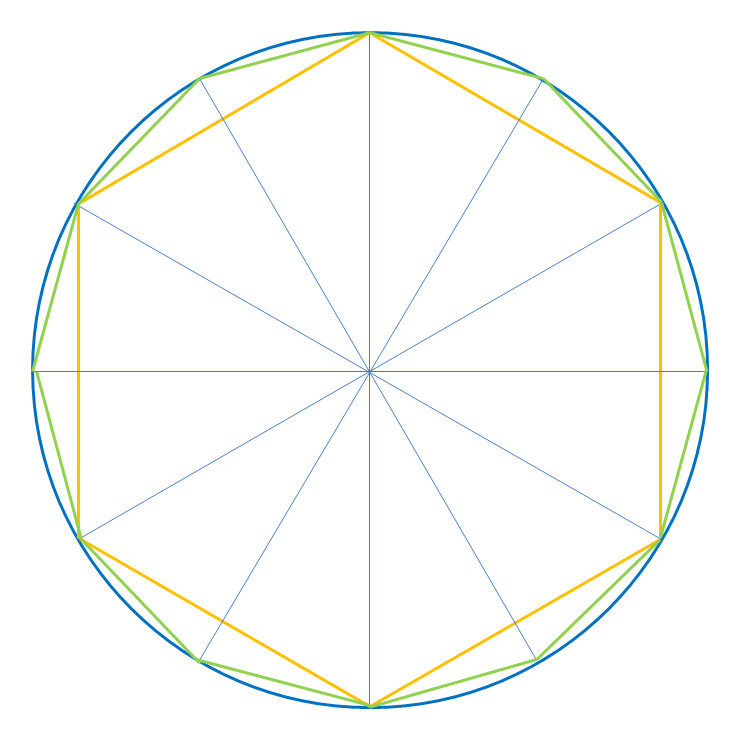
In einen Kreis wird ein regelmässiges Sechseck gezeichnet. Der Radius des Kreises sei 1.
Das Sechseck kann man sich aus 6 gleichseitigen Dreiecken mit der Seite 1 denken.
Wird nun die Sechseck-Linie als erste Annäherung an die Kreislinie gesehen, erhalten wir einen Umfang von u = 6.
Die Kreis-Umfangsformel u = 2 r π wird nun nach π aufgelöst (beide Seiten dividieren durch 2r).
r ist 1. Pi wird somit in der ersten Annäherung geschätzt als π = 6 / 2 = 3
Pi wird genauer, wenn wir den Umfang eines 12-Ecks berechnen. Wir sehen, dass sich die grüne 12-Eck-Linie schon viel näher an die Kreislinie anschmiegt.
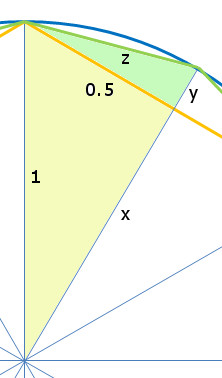
In der Abbildung rechts sehen wir, wie man die 12-Eck-Seite berechnet:
Der Radius ist gleich 1.
Die Radien und die 6-Eck-Seite bilden zwei rechtwinklige Dreiecke.
Schritt 1
Die Kathete x kann mit dem Pythagoras berechnet werden: x = Wurzel (12 – 0.52) = 0.866025404
Schritt 2
Die Kathete y ist die Differenz zwischen dem Radius 1 und x. y = 0.133974596
Schritt 3
Nun kann mit den beiden bekannten Katheten die Hypotenuse z (12-Ecks-Seite) berechnet werden: z = Wurzel (0.52 + y2) = 0.51763809
Annäherung von Pi mit dem 12-Eck
Zwölfeck-Umfang u = 2 r π
π ≈ 3.10582854123025
Annäherung an π bis zu einem sehr genauen Wert
Um einen genauen Wert von Pi zu erhalten, müssen nun schrittweise die Ecken verdoppelt werden. Wie schon vorher ein 12-Eck aus dem 6-Eck gewonnen wurde, kann nun ein 24-Eck berechnet werden, danach ein 48-Eck usw. Also
6-Eck
12-Eck
24-Eck
48-Eck
96-Eck
192-Eck
….
….
Von Hand eine aufwändige Sache… Darum zeige ich auf der nächsten Seite:
Wie man Pi mit einem Tabellen-Kalkulationsprogramm berechnet.