Alles begann mit dem Zählen

Das erste Hilfsmittel für das Erfassen der Zahlen und die Verarbeitung von Dinge und Waren waren wohl unsere menschlichen Hände mit ihren zehn Fingern.
Der Wolfsknochen aus Tschechien
In der gut untersuchten Mammutjägersiedlung Dolni Vestonice wurde ein 18 cm langer Wolfsknochen gefunden, welcher mit einem Alter von 25 – 30’000 Jahren die älteste bis jetzt bekannte Zahlendarstellung zeigt.

Auf der einen Seite sind 25 Kerben, auf der anderen 30 Kerben zu sehen. Es scheint sogar eine 5-er Bündelung zu geben. Offenbar war es einem Menschen vor 30’000 Jahren wichtig, eine Zahl auf dem Knochen zu fixieren.
Der Ishango-Knochen
Das Zählen ist die erste mathematische Leistung, die man bereits vor 20’000 Jahren in der Cro-Magnon-Zeit vorgefunden hat. Auch auf diesem Knochen sind Kerben erkennbar, die eine Fünferbündelung aufweisen.

Abbildung Ishango-Knochen von vorne und von hinten aus der DR Kongo
Kerbholz, Kerbstock, Zählholz oder Zählstab (tally sticks)

Sogenannte Kerbhölzer gab es auch später noch. Sie dienten vor allem zum Festhalten von Schulden.
Auf einem Stück Holz wurden Kerben angebracht, um die Schulden darzustellen oder zum Beispiel festzuhalten, wie viel Stück Vieh einem Hirten anvertraut worden sind. Dann wurde dieses Kerbholz längs in zwei Stücke gespalten, dass der Schuldner und der Gläubiger einen Beleg für die Schulden hatten. Fügte man diese beiden Stücke wieder zusammen, konnte einfach belegt werden, ob die beiden Stücke zusammengehören, oder ob das Kerbholz nachträglich manipuliert worden war.
Am Zahltag konnte das Kerbholz präsentiert werden, um die Schulden zu begleichen.

In Europa wurden Kerbhölzer (in England: Tally sticks) noch bis weit ins 19. Jahrhundert verwendet. Sie halfen auch den Analphabeten, einfach verständliche Belege zu erhalten.

Aus dem Wallis gibt es auch schöne Kerbholz-Beispiele, die bis ins 20. Jahrhundert von der Alp-Bevölkerung gebräuchlich waren. Hier wurden sie Tesseln oder Tässle genannt und hielten Wasser-, Kuh-, Alprechte und dergleichen fest.
„Etwas auf dem Kerbholz haben“
Noch heute kennen wir die Redewendung „etwas auf dem Kerbholz haben„. Es bedeutet, dass wir etwas Unerlaubtes getan haben oder sogar eine Straftat begangen haben, also sich schuldig gemacht haben.
Strichlisten wie beim Jassen (Kartenspiel)
Strichlisten, wie wir sie auf Kerbhölzern finden, brauchen wir noch heute zum Beispiel beim Spiel:
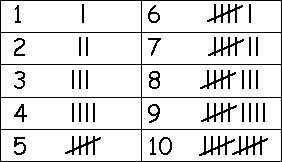
Uralte Zählsteine

Neben der geritzten Zählknochen oder Kerbhölzer gibt es auch Zählsteine, die bereits in den frühen Kulturen wie in Assyrien gefunden wurden.
In Babylon (1800 v. Chr.) zählten sie mit einem 60-er Zahlensystem
In Babylon und anderen Zentren der vorderasiatischen Region begannen sich vor 5000 Jahren Hochkulturen zu bilden. Zählen von Vieh und sonstigen Waren wurde nötig.
Das Zahlensystem der Babylonier ist das 60-er System, auch bekannt als das sexagesimale System. Es handelt sich um ein Zahlensystem, das auf der Basis 60 aufbaut, im Gegensatz zum heute gebräuchlichen dezimalen System, das auf der Basis 10 aufbaut.
Im 60-er System wurden Zahlen durch verschiedene Zeichen dargestellt. Die Zeichen wurden in Gruppen von 1 bis 59 verwendet, und wenn eine grössere Zahl dargestellt werden musste, wurden mehrere Zeichen hintereinander geschrieben.

Die Babyloner hatten spezielle Zeichen für die Zahlen 1 bis 59. Diese Zeichen waren oft Kombinationen aus Keilschriftzeichen und Linien. Das Zeichen für die Zahl 1 wurde einfach durch eine einzelne Keilschriftlinie dargestellt, während die Zahl 10 durch ein anderes Zeichen repräsentiert wurde. Ähnlich wie im dezimalen System wurde das System dann fortgesetzt, indem Zeichen für die Zahlen 20, 30, 40 usw. verwendet wurden.
Die Babyloner waren auch in der Lage, Brüche und Teilungen im 60-er System darzustellen. Zum Beispiel wurde die Hälfte, also 30, durch ein spezielles Zeichen dargestellt. Ein Viertel entsprach 15 und wurde ebenfalls durch ein eigenes Zeichen dargestellt. Das System war daher recht flexibel und ermöglichte es den Babyloniern, verschiedene mathematische Operationen durchzuführen.
Ein weiterer Vorteil des 60-er Systems war, dass es gut zur Darstellung von Winkeln geeignet war. Ein voller Kreis wurde in 360 Grad unterteilt, was wiederum auf der Basis 60 basierte. Dieses Masssystem für Winkel wird heute noch in der Geometrie verwendet.
Obwohl das 60-er System im Alltag der Babyloner weit verbreitet war, ist es im modernen Leben weniger gebräuchlich geworden. Das dezimale System mit der Basis 10 hat sich in den meisten Kulturen durchgesetzt. Dennoch hat das 60-er System einen bleibenden Einfluss hinterlassen und wird heute noch in bestimmten Bereichen wie der Zeitmessung (60 Sekunden in einer Minute, 60 Minuten in einer Stunde) und der Winkelberechnung verwendet.
Ägypten
Die ägyptischen Zahlen sind aus Hieroglyphen aufgebaut:

Die Mathematik der alten Ägypter war bemerkenswert fortgeschritten und hatte einen starken praktischen Fokus. Die Ägypter verwendeten Mathematik für verschiedene Zwecke, wie zum Beispiel Landvermessung, Bauwesen, Handel und sogar astronomische Berechnungen.
Die Ägypter verwendeten ein dezimales Zahlensystem, das auf der Basis 10 aufbaute. Sie hatten spezielle Hieroglyphen, um Zahlen von 1 bis 9 darzustellen. Für grössere Zahlen wurden diese Hieroglyphen einfach wiederholt. Obwohl die Ägypter keine spezifische Schrift für Null hatten, konnten sie leere Stellen verwenden, um den Platzwert auszudrücken.
Die Ägypter waren sehr geschickt im Umgang mit Brüchen. Sie kannten Brüche wie 1/2, 1/3, 2/3, 1/4 und 3/4 und hatten spezielle Symbole, um diese darzustellen. Sie waren in der Lage, Brüche zu addieren, zu subtrahieren und zu multiplizieren, und sie hatten sogar Techniken zur Berechnung von Bruchteilen einer Einheit.
Die ägyptische Geometrie konzentrierte sich hauptsächlich auf Flächen- und Volumenberechnungen. Die Ägypter kannten bereits die Berechnung von Flächen für einfache geometrische Formen wie Rechtecke, Dreiecke und Trapeze. Sie waren in der Lage, die Volumina von rechtwinkligen Prismen und Zylindern zu berechnen und verwendeten diese Kenntnisse beispielsweise beim Bau von Pyramiden und Gräbern.
Die Ägypter verwendeten auch einfache algebraische Techniken zur Lösung von Gleichungen. Sie konnten lineare Gleichungen mit einer Unbekannten lösen, indem sie beide Seiten schrittweise umkehrten und vereinfachten.
In der Astronomie verwendeten die Ägypter mathematische Kenntnisse, um den Himmel zu beobachten und Kalender zu erstellen. Sie konnten beispielsweise den jährlichen Zyklus der Überschwemmungen des Nils mithilfe astronomischer Beobachtungen vorhersagen.
Ein bekanntes mathematisches Dokument aus dem alten Ägypten ist das „Moskauer Papyrus“, das verschiedene mathematische Probleme und Aufgaben enthält, einschliesslich geometrischer Berechnungen und Bruchrechnungen.
Die Mathematik der alten Ägypter war zwar nicht so formal und abstrakt wie die heutige Mathematik, aber sie war äusserst praktisch und gut entwickelt. Ihre mathematischen Fähigkeiten trugen zur Entwicklung ihrer beeindruckenden Bauwerke, zur Landwirtschaft, zum Handel und zur Organisation ihrer Gesellschaft bei.
Indien – vedische Mathematik
Die vedische Mathematik ist ein antikes indisches mathematisches System, das auf den vedischen Schriften basiert, einer Sammlung religiöser und philosophischer Texte aus dem alten Indien. Diese Mathematik entwickelte sich zwischen dem 1. Jahrtausend v. Chr. und dem 5. Jahrhundert n. Chr. und wurde von den Brahmanen, einer hinduistischen Priesterkaste, praktiziert.
Die vedische Mathematik zeichnet sich durch ihre Einfachheit, Effizienz und Systematik aus. Sie basiert auf einer Reihe von Sutras (Regeln) und Subsutras (Unterregeln), die als kurze und prägnante Aussagen formuliert sind. Diese Sutras und Subsutras dienen als Grundlage für die Durchführung von mathematischen Operationen.
Ein wichtiges Konzept der vedischen Mathematik ist das „Vertikal-und-Quer-Multiplizieren“. Hierbei werden die Ziffern der beiden zu multiplizierenden Zahlen in einer vertikalen Struktur angeordnet, und die Produkte werden horizontal berechnet. Dieses Verfahren ermöglicht es, Multiplikationen schnell und einfach durchzuführen.
Ein weiteres bemerkenswertes Konzept der vedischen Mathematik ist das „Nikhilam-Sutra“ oder das „allumfassende Sutra“. Es ermöglicht das Durchführen von Multiplikationen und Divisionen durch das Hinzufügen oder Entfernen von Basen und Ausgleichen durch geeignete Anpassungen. Dieses Konzept ist nützlich für Berechnungen mit grossen Zahlen.
Die vedische Mathematik enthält auch Techniken für das quadratische Wurzelziehen, die Berechnung von Brüchen, die Teilung von Zahlen und vieles mehr. Es wurden sogar Methoden entwickelt, um die Trigonometrie und die Anwendung auf astronomische Berechnungen zu behandeln.
Die vedische Mathematik hatte einen grossen Einfluss auf die Mathematik des antiken Indiens und darüber hinaus. Ihre Methoden und Techniken wurden in verschiedenen Schriften dokumentiert und weiterentwickelt. Viele ihrer Ideen und Prinzipien finden sich auch in modernen mathematischen Konzepten wieder.
Die vedische Mathematik hat bis heute eine grosse Bedeutung. Sie wird in Indien und anderen Teilen der Welt gelehrt und angewendet, und ihre Methoden werden oft zur Verbesserung der mathematischen Fähigkeiten von Schülern verwendet.
Warum sind viele Inder so schnell im Kopfrechnen? Das mag seinen Grund in der vedischen Mathematik haben. Es ist zwar umstritten, ob sich diese schlauen Rechenmethoden, welche Strukturen beachten, sich wirklich auf der heilige Lehre des Veda gründen. Genial und trickreich sind sie allemal!
Einige Beispiele seien hier exemplarisch gezeigt:
Subtraktion von beliebigen Zahlen von einer Zehnerpotenz
In der vedischen Mathematik gibt es eine spezielle Methode, um beliebige Zahlen von einer Zehnerpotenz zu subtrahieren. Diese Methode basiert auf dem Konzept des „Vertikal-und-Quer-Sutra“ und ermöglicht es, Subtraktionen schnell und effizient durchzuführen.
Um eine Zahl von einer Zehnerpotenz zu subtrahieren, folge diesen Schritten:
Schritt 1: Wähle eine Zehnerpotenz, von der du die Zahl subtrahieren möchtest. Runde die gegebene Zahl auf die nächstniedrigere Zehnerpotenz ab.
Schritt 2: Schreibe die abgerundete Zahl unter die Zehnerpotenz, von der du subtrahierst. Lasse eine leere Spalte zwischen beiden Zahlen.
Schritt 3: Subtrahiere jede Ziffer der abgerundeten Zahl von 9 und schreibe das Ergebnis in der leeren Spalte.
Schritt 4: Beginne von rechts und subtrahiere die entsprechenden Ziffern vertikal voneinander. Schreibe das Ergebnis unter der leeren Spalte.
Schritt 5: Führe eventuell auftretende Überträge (wenn das Ergebnis grösser als 9 ist) nach links durch.
Schritt 6: Das Endergebnis ist die Kombination der in Schritt 5 erhaltenen Zahlen.
Hier ist ein Beispiel, um die Methode zu veranschaulichen:
Subtrahiere 186 von 1000.
Schritt 1: Die nächstniedrigere Zehnerpotenz ist 100. Runde 186 auf die nächstniedrigere Zehnerpotenz ab, was 100 ergibt.
Schritt 2: Schreibe 100 unter 1000 und lasse eine leere Spalte dazwischen:
1000
100
Schritt 3: Subtrahiere jede Ziffer von 9:
1000
100
899
Schritt 4: Subtrahiere die Ziffern vertikal:
1000
100
899
814
Schritt 5: Es tritt kein Übertrag auf.
Schritt 6: Das Endergebnis ist 814.
Das Ergebnis der Subtraktion von 186 von 1000 mit der vedischen Methode ist 814.
Subtraktion beliebiger Zahlen durch Ergänzung
Multiplikation zweistelliger Zahlen
Quadrieren von Zahlen mit Endziffer 5
Multiplikation von Zahlen, die nahe an einer Zehnerpotenz liegen
China
Die Mathematik im alten China hat eine lange und reiche Geschichte, die sich über Tausende von Jahren erstreckt. Die chinesische Mathematik entwickelte sich parallel zu anderen Wissenschaften und spielte eine wichtige Rolle in verschiedenen Bereichen wie Astronomie, Kalenderberechnungen, Landvermessung, Handel und Musik.
Ein bedeutendes Werk in der chinesischen Mathematik ist das „Jiuzhang Suanshu“ oder „Neun Bücher der mathematischen Kunst“. Es ist eine Sammlung mathematischer Texte aus verschiedenen Zeiträumen und behandelt verschiedene mathematische Themen wie Arithmetik, Algebra, Geometrie und Trigonometrie. Diese Bücher enthalten eine Vielzahl von mathematischen Problemen, Lösungsmethoden und Berechnungstechniken.
Die chinesische Mathematik verwendete ein dezimales Zahlensystem, ähnlich dem heute verwendeten. Die Chinesen hatten spezielle Schriftzeichen, um Zahlen darzustellen, und kannten die vier Grundrechenarten: Addition, Subtraktion, Multiplikation und Division. Sie entwickelten auch spezielle Rechengeräte wie den Abakus, der noch heute in einigen Teilen Chinas verwendet wird.
Ein bemerkenswerter Beitrag der chinesischen Mathematik ist das „Pascal’sche Dreieck“, das auch in anderen Kulturen bekannt ist. Dieses Muster von Zahlen, das sich durch die Addition der beiden Zahlen darüber ergibt, wurde bereits im 13. Jahrhundert v. Chr. von chinesischen Mathematikern beschrieben.
Die chinesische Mathematik war auch stark mit der Astronomie verbunden. Die alten Chinesen führten astronomische Beobachtungen durch und entwickelten Kalendersysteme, um die Bewegungen von Sonne, Mond und Sternen vorherzusagen. Dies erforderte komplexe mathematische Berechnungen, um Positionen, Zeiträume und Phänomene zu bestimmen.
Die chinesische Mathematik hatte einen starken praktischen Fokus und konzentrierte sich auf konkrete Anwendungen. Die Chinesen entwickelten Methoden zur Berechnung von Flächen, Volumina, Wurzeln und trigonometrischen Funktionen. Sie verwendeten auch Proportionen und Verhältnisse, um Probleme zu lösen und Beziehungen in verschiedenen Bereichen zu verstehen.
Die Mathematik im alten China hatte einen grossen Einfluss auf andere Kulturen, insbesondere auf die islamische und europäische Mathematik. Viele mathematische Konzepte und Techniken, die in China entwickelt wurden, fanden ihren Weg in die Welt und trugen zur Entwicklung der modernen Mathematik bei.
Griechenland
Die Mathematik im antiken Griechenland hatte einen enormen Einfluss auf die Entwicklung der Mathematik und trug zur Grundlegung vieler mathematischer Konzepte bei, die bis heute relevant sind. Die griechische Mathematik blühte zwischen dem 6. Jahrhundert v. Chr. und dem 4. Jahrhundert n. Chr.
Die griechische Mathematik war stark von der Philosophie und dem rationalen Denken der Zeit geprägt. Sie war weniger praktisch orientiert als die Mathematik in anderen Kulturen und legte den Schwerpunkt auf Beweise und logische Argumentation.
Einer der bekanntesten Mathematiker des antiken Griechenlands war Pythagoras, der nach ihm benannte Satz (Pythagoreischer Satz) ist weltbekannt. Pythagoras und seine Schüler entwickelten ein Verständnis für Zahlen und deren Eigenschaften, insbesondere im Zusammenhang mit geometrischen Figuren. Sie glaubten auch an die Bedeutung von Harmonie und Musik in der Mathematik.
Ein weiterer prominenter Mathematiker war Euklid, dessen Werk „Elemente“ zu den einflussreichsten mathematischen Werken der Geschichte gehört. In den „Elementen“ stellte Euklid die Grundlagen der Geometrie dar und entwickelte eine systematische Herangehensweise an Beweise und mathematische Argumentation. Sein Werk hatte einen enormen Einfluss auf die mathematische Entwicklung und wurde über Jahrhunderte hinweg studiert.
Ein weiterer bedeutender Mathematiker war Archimedes, der sich mit Berechnungen von Flächen, Volumina und Kräften beschäftigte. Er entwickelte innovative Methoden zur Bestimmung von Flächeninhalten und Volumina, einschliesslich der Methode der Erschöpfung. Archimedes gilt auch als einer der Begründer der Infinitesimalrechnung.
Die griechischen Mathematiker leisteten auch wichtige Beiträge zur Trigonometrie und zur Entwicklung des logarithmischen Systems. Hipparchos von Nikäa entwickelte trigonometrische Tabellen und führte die Verwendung von trigonometrischen Funktionen in der Astronomie ein. Die Verwendung von logarithmischen Funktionen wurde von Heron von Alexandria erforscht.
Die Mathematik im antiken Griechenland hatte einen starken Einfluss auf die westliche Mathematiktradition. Viele Konzepte und Methoden, die von den griechischen Mathematikern entwickelt wurden, wurden von späteren Mathematikern weiterentwickelt und bildeten die Grundlage für die moderne Mathematik. Die Betonung von Beweisen und logischer Argumentation ist auch heute noch ein wichtiger Bestandteil der mathematischen Forschung und Lehre.
Die Mathematik der Römer
Die römische Mathematik entwickelte sich während des Römischen Reiches (ca. 753 v. Chr. bis 476 n. Chr.) und war stark von den griechischen mathematischen Ideen beeinflusst. Die Römer übernahmen viele mathematische Konzepte und Techniken von den Griechen und trugen gleichzeitig mit eigenen Beiträgen zur Entwicklung der Mathematik bei.
In der römischen Mathematik lag der Schwerpunkt vor allem auf praktischen Anwendungen und Problemlösungen im Alltag, insbesondere in den Bereichen Handel, Architektur, Vermessung und Ingenieurwesen.

Diese Inschrift gibt an, dass das Gebäude 1780 gebaut wurde.
Die Zahlen der Römer sind abgeleitet von der menschlichen Hand. Ab der Zahl 50 werden Abkürzungen für die Zahlennamen benutzt.
| römische Zahl | arabische Zahl | Herkunft oder Erklärung |
| I | 1 | ein Finger |
| II | 2 | zwei Finger |
| III | 3 | drei Finger |
| IV | 4 | eins weniger als eine Hand |
| V | 5 | eine Hand |
| VI | 6 | eine Hand und ein Finger |
| VII | 7 | eine Hand und zwei Finger |
| VIII | 8 | eine Hand und drei Finger |
| IX | 9 | eins weniger als zwei Hände |
| X | 10 | zwei Hände |
| L | 50 | halbes Hundert |
| C | 100 | von centum (Hundert) |
| D | 500 | |
| M | 1000 | von milia (Tausend) |
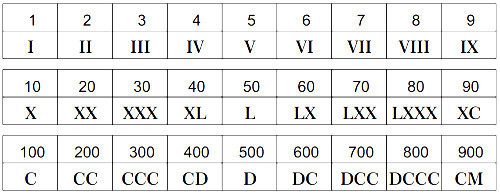
Hunderter, Zehner, Einer werden einzeln aneinandergereiht.
Das römische Zahlensystem war additiv aufgebaut, d. h. die Zahlen wurden durch Hinzufügen der Symbole aufgebaut. Subtraktion wurde ebenfalls verwendet, indem ein kleineres Symbol vor einem grösseren platziert wurde (z. B. IV für 4).
Die römische Mathematik konzentrierte sich hauptsächlich auf die vier Grundrechenarten: Addition, Subtraktion, Multiplikation und Division. Die Römer entwickelten spezielle Rechenmethoden für das Addieren und Subtrahieren von römischen Zahlen. Für die Multiplikation und Division wurden hingegen häufig das Rechenbrett (abacus) und Abakus verwendet, die auf dem Prinzip der Stellenwertsysteme basierten.
Ein bekannter römischer Mathematiker war Marcus Vitruvius Pollio, auch bekannt als Vitruvius. Er war ein Architekt und Ingenieur, der das Werk „De Architectura“ verfasste, in dem er mathematische Prinzipien auf Architektur und Bauwesen anwendete. Vitruvius beschrieb geometrische Konzepte wie die Berechnung von Flächeninhalten, das Konstruieren von Kreisen und die Nutzung von Proportionen in der Architektur.
Die römische Mathematik hatte jedoch im Vergleich zu den Griechen und anderen Kulturen keine grossen mathematischen Durchbrüche erzielt. Sie legte den Schwerpunkt eher auf praktische Anwendungen und war weniger theoretisch orientiert. Dennoch trug die römische Mathematik zur Entwicklung des römischen Reiches bei, indem sie die Grundlagen für Bauwerke, Handel und Vermessungen legte.
Es ist wichtig zu beachten, dass die römische Mathematik im Vergleich zu anderen antiken Kulturen wie den Griechen und den Ägyptern weniger bekannt ist, da viele mathematische Werke der Römer nicht erhalten geblieben sind. Die meisten Informationen über römische Mathematik stammen aus späteren Schriften und Texten anderer Kulturen, die über römische mathematische Ideen berichteten.
Arabische Mathematik und Zahlen
Die arabische Mathematik bezieht sich auf die mathematischen Entwicklungen, die im arabischen Kulturraum vom 8. bis zum 14. Jahrhundert stattfanden. Während dieser Zeit erreichte die arabische Welt ein bemerkenswertes Niveau in der Mathematik und übernahm viele mathematische Konzepte und Erkenntnisse aus anderen Kulturen wie den Griechen, Indern und Persern. Die arabischen Mathematiker machten jedoch auch eigene originelle Beiträge zur Mathematik.
Einer der bekanntesten und einflussreichsten Mathematiker dieser Zeit war Muhammad ibn Musa al-Khwarizmi, dessen Name den Begriff „Algorithmus“ inspirierte. Al-Khwarizmi schrieb das Buch „Kitab al-Jabr wa al-Muqabala“ (Das Buch der Wiederherstellung und der Rechtsregeln), das eine systematische Behandlung von Algebra und Gleichungen enthielt. In diesem Werk entwickelte er algebraische Methoden zur Lösung von linearen und quadratischen Gleichungen und legte damit die Grundlagen für die moderne Algebra.
Ein weiterer wichtiger Beitrag der arabischen Mathematik war die Einführung des Dezimalsystems und der Stellenwertnotation, die auf indischen Zahlen basierten. Die Araber erkannten den enormen Vorteil dieses Systems, das auf der Verwendung von Ziffern und Platzhaltern beruht, und trugen zur Verbreitung dieses Zahlensystems im westlichen Raum bei. Sie entwickelten auch Methoden für arithmetische Operationen, einschliesslich Addition, Subtraktion, Multiplikation und Division mit dezimalen Brüchen.
Arabische Mathematiker machten auch Fortschritte in der Trigonometrie. Sie übernahmen das Wissen der Griechen und der Inder und entwickelten neue trigonometrische Funktionen und Tabellen. Diese Fortschritte in der Trigonometrie waren wichtig für astronomische Berechnungen und Navigation.
Ein weiteres bemerkenswertes Werk der arabischen Mathematik ist das „Buch der Optik“ des Mathematikers und Astronomen Ibn al-Haytham. In diesem Werk untersuchte er die Optik und das Phänomen des Lichts und legte damit den Grundstein für die moderne Physik.
Die arabische Mathematik hatte einen grossen Einfluss auf die Entwicklung der Mathematik im mittelalterlichen Europa. Die arabischen mathematischen Werke wurden ins Lateinische übersetzt und bildeten eine Brücke zwischen der antiken griechischen Mathematik und der europäischen Renaissance. Viele mathematische Konzepte und Techniken, die von den Arabern entwickelt wurden, wie etwa das Dezimalsystem und algebraische Methoden, wurden von europäischen Mathematikern weiterentwickelt und trugen zur Entstehung der modernen Mathematik bei.
Mittelalter
Die Mathematik im Mittelalter, auch als mittelalterliche Mathematik bezeichnet, umfasst den Zeitraum vom 5. bis zum 15. Jahrhundert in Europa. Während dieser Zeit erlebte Europa eine Periode des gesellschaftlichen Wandels, der politischen Instabilität und des Fortschritts in verschiedenen Wissensbereichen, einschließlich der Mathematik.
In den frühen Jahren des Mittelalters waren die mathematischen Kenntnisse in Europa begrenzt und wurden größtenteils von arabischen und griechischen Quellen übernommen. Arabische mathematische Texte wurden aus dem Arabischen ins Lateinische übersetzt, was dazu beitrug, das mathematische Wissen im mittelalterlichen Europa zu erweitern.
Eine wichtige Entwicklung in der mittelalterlichen Mathematik war die Verbreitung der hindu-arabischen Zahlschrift und des Dezimalsystems, die von den Arabern eingeführt worden waren. Dieses Zahlsystem mit den Ziffern 0 bis 9 und der Verwendung von Platzhaltern revolutionierte das Rechnen und erleichterte komplexe Berechnungen. Es ermöglichte eine effizientere Verwendung von Zahlen und die Durchführung von Rechenoperationen wie Addition, Subtraktion, Multiplikation und Division.
Im Laufe des Mittelalters begannen europäische Mathematiker, eigene Beiträge zu leisten und mathematische Konzepte weiterzuentwickeln. Ein herausragender Mathematiker dieser Zeit war Leonardo Fibonacci, auch bekannt als Fibonacci, der im 13. Jahrhundert lebte. Fibonacci war bekannt für seine Arbeit zur Vermittlung des Hindu-Arabischen Zahlensystems und der Fibonacci-Folge, einer Zahlenreihe, die in vielen natürlichen Phänomenen vorkommt.
Eine weitere wichtige Entwicklung in der mittelalterlichen Mathematik war die Einführung der Algebra als eigenständige Disziplin. Die Algebra befasste sich mit der Untersuchung von Gleichungen, Symbolen und Variablen. Mathematiker wie Robert von Chester und Jordanus de Nemore trugen zur Entwicklung der algebraischen Methoden bei und verfassten mathematische Abhandlungen, in denen sie Probleme der Algebra behandelten.
Darüber hinaus spielte die Geometrie eine bedeutende Rolle in der mittelalterlichen Mathematik. Mathematiker wie Johannes Sacrobosco, bekannt für sein Werk „Tractatus de Sphaera“, beschäftigten sich mit geometrischen Konzepten wie der Berechnung von Flächen und Volumen sowie der Untersuchung der Himmelskörper.
Die mathematischen Kenntnisse im Mittelalter wurden hauptsächlich von Mönchen, Gelehrten und Universitäten gepflegt und weitergegeben. Die mittelalterliche Mathematik war stark mit anderen Wissensbereichen wie der Astronomie, der Musik, der Philosophie und der Theologie verbunden.
Es ist wichtig anzumerken, dass die mittelalterliche Mathematik von der Mathematik der Antike und der Mathematik der Renaissance umgeben war und einen Übergang zwischen diesen beiden Epochen darstellte. Viele der mathematischen Entwicklungen im Mittelalter legten den Grundstein für die späteren mathematischen Fortschritte und bildeten die Basis für die Entwicklung der modernen Mathematik.
Mathematik der Neuzeit
Die Mathematik der Neuzeit bezieht sich auf die Entwicklung der Mathematik ab dem 16. Jahrhundert bis zur Gegenwart. Diese Zeitperiode wird oft als Beginn der modernen Mathematik angesehen, in der wichtige mathematische Konzepte und Theorien entwickelt wurden, die bis heute von großer Bedeutung sind.
Ein bedeutender Wendepunkt in der Mathematikgeschichte der Neuzeit war die Entstehung der Infinitesimalrechnung, die unabhängig voneinander von Isaac Newton und Gottfried Wilhelm Leibniz entwickelt wurde. Die Infinitesimalrechnung legte den Grundstein für die Analyse und ermöglichte die mathematische Beschreibung von Veränderungen und kontinuierlichen Prozessen. Diese Entwicklung war von entscheidender Bedeutung für die Physik und viele andere Wissenschaften.
Im 17. und 18. Jahrhundert spielte die Mathematik eine wichtige Rolle bei der Erforschung der Naturgesetze und der Entdeckung neuer mathematischer Prinzipien. Mathematiker wie Leonhard Euler, Carl Friedrich Gauss und Pierre-Simon Laplace trugen zur Entwicklung der Zahlentheorie, der Analysis, der Geometrie und der Wahrscheinlichkeitstheorie bei. Ihre Arbeiten legten den Grundstein für viele mathematische Gebiete, die bis heute erforscht werden.
Im 19. Jahrhundert wurden weitere bedeutende Fortschritte in der Mathematik erzielt. Der Mathematiker Augustin-Louis Cauchy entwickelte rigorose Beweismethoden für die Analysis, während der deutsche Mathematiker Georg Cantor die Theorie der Mengen und die Konzepte des Unendlichen weiterentwickelte. Auch die Entdeckung der nichteuklidischen Geometrien durch Nikolai Lobatschewski und János Bolyai revolutionierte das Verständnis der Geometrie.
Im 20. Jahrhundert erlebte die Mathematik eine explosive Entwicklung, insbesondere durch die Entstehung der mathematischen Logik, der abstrakten Algebra, der Topologie und der Kategorientheorie. Mathematiker wie David Hilbert, Kurt Gödel, Alan Turing und John von Neumann prägten diese Zeit mit ihren wegweisenden Beiträgen. Die Mathematik wurde immer abstrakter und rigoroser und fand Anwendungen in vielen Bereichen wie Physik, Informatik, Ökonomie und Kryptographie.
In der Gegenwart setzt sich die Entwicklung der Mathematik fort, wobei immer neue Gebiete erforscht und neue Anwendungen entdeckt werden. Die moderne Mathematik befasst sich mit hochkomplexen Strukturen, algorithmischen Methoden, Künstlicher Intelligenz, Big Data und vielem mehr. Mathematiker arbeiten eng mit Wissenschaftlern aus verschiedenen Disziplinen zusammen und tragen maßgeblich zu technologischen Fortschritten und wissenschaftlicher Erkenntnis bei.
Die Mathematik der Neuzeit hat die Grundlagen für viele andere Wissenschaften gelegt und spielt eine entscheidende Rolle in unserer modernen Gesellschaft. Sie ist nicht nur eine abstrakte Wissenschaft, sondern auch ein Werkzeug, das in vielen Bereichen angewendet wird, um komplexe Probleme zu lösen und neue Erkenntnisse zu gewinnen.