Zahlengleichungen oder Ungleichungen mit Zahlen sind Aussagen.
3 + 7 = 2 + 8 Gleichung
3 + 7 < 3 + 8 Ungleichung
Aussagen sind entweder wahr oder falsch.
Bestimmungsgleichungen oder Bestimmungs‑Ungleichungen sind Aussageformen. Sie enthalten Variablen.
8x + 2 = 18 Gleichung
32 – x > 19 Ungleichung
Werden die Variablen durch Zahlen ersetzt, geht die Aussageform in eine Aussage über.
Aussage: Eine Aussage ist ein Sachverhalt, der eindeutig entweder wahr oder falsch ist. Mathematisch gesehen sind es zwei Terme, die durch ein Gleichheits- oder Ungleichheitszeichen verbunden sind.
Beispiele
A. Brüssel ist die Hauptstadt von Belgien.
B. Moskau ist die Hauptstadt von China.
C. 3 + 4 = 7
D. 12 < 7
Die Aussage A ist wahr, der Wahrheitsgehalt von A ist wahr, oder w(A) = wahr
Die Aussage B ist falsch, der Wahrheitsgehalt von B ist falsch, oder w(B) = falsch
Die Aussage C ist wahr, der Wahrheitsgehalt von D ist falsch, oder w(C) = wahr
Die Aussage D ist falsch, der Wahrheitsgehalt von C ist falsch, oder w(D) = falsch
Keine Aussagen im mathematischen Sinne sind:
- Guten Tag
- Lieben Sie Gulasch?
- Nachts wird es mir zu kalt.
- Morgen werden wir die Mathematik begreifen.
Warum sind das keine Aussagen?
- Weil wir den Wahrheitsgehalt nicht prüfen können.
- Weil sie nicht aus zwei Termen bestehen, deren Vergleich einer Wahrheitsprüfung unterzogen werden kann.
Gleichungen
Unter einer Gleichung versteht man in der Mathematik eine Aussage über die Gleichheit zweier Terme oder Sachverhalte, die mit Hilfe des Gleichheitszeichens („=“) symbolisiert wird.
Wir können sie mit einer Waage vergleichen
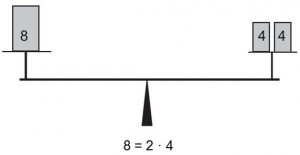
Ungleichungen
Entsprechend hat bei einer Ungleichung die Ungleichheit zweier Terme. Hier stehen anstelle des Gleichheitszeichens die Zeichen:
< kleiner als
> grösser als
≤ kleiner gleich nicht grösser als höchstens
≥ grösser gleich nicht kleiner als mindestens
≠ ungleich verschieden
Bei den (Un)Gleichungen unterscheidet man
- Zahlen(un)gleichungen (ohne Variablen)
- Bestimmungs(un)gleichungen (mit Variablen, die bestimmt werden können)
Gleichungen lösen (Äquivalenzumformungen)
- Terme (Ausdrücke) vereinfachen
- Addition bzw. Subtraktion der gleichen Zahl oder des gleichen Terms auf beiden Seiten
- Multiplikation mit der gleichen Zahl (ausser 0) oder mit dem gleichen (von 0 verschiedenen) Term auf beiden Seiten
- Division durch die gleiche Zahl (ausser 0) oder durch den gleichen (von 0 verschiedenen) Term auf beiden Seiten
- Seiten vertauschen
Übungen
Ist es eine Aussage, eine Aussageform oder nix?
- Die Arbeitslosenzahl dieses Jahr ist grösser als letztes Jahr.
- Wer war Clara Wieck?
- Helfen Sie mir doch!
- Eine Zahl, die kleiner als Null ist, heisst “negativ”.
- Joggen hält fit.
- Schlangen sind keine Säugetiere.
- 2 + 2 = 5.
- Es gibt ausserirdische Lebewesen
- Heute scheint wieder einmal die Sonne.
- Das Haus hat rote Fensterläden.
- Pisa ist eine Stadt in Italien.
- Die Industrialisierung schafft für viele Menschen eine höhere Lebensqualität!
- Rote Rosen sind schön.
- 2 + x = 5.
- Ich mag keine Spaghetti!
Ist die Aussage wahr oder falsch?
- a) 6 · 3 – 4 =14 (w) ; dies ist eine wahre Aussage
- b) 3 · (-2) + 4 = 4 · (-2) – 1 (f) ; dies ist eine falsche Aussage
- c) 10 =10 (w) ; dies ist eine wahre Aussage
- d) 4 = 3 (f) ; dies ist eine falsche Aussage
Textgleichungen
Max und Roger prahlen mit der Menge SMS, die sie Tag für Tag versenden. Max hat gestern 25 SMS verschickt. Das sind 7 SMS mehr als die dreifache Menge von Roger. Wie viele SMS hat Roger gestern verschickt?
Lösung
(25 – 7) = 3x
18 = 3x
x = 6
Max versendet 25 SMS
Roger versendet 6 SMS
6 * 3 = 18 Max versendet drei mal mehr…
18 + 7 = 25 Max versendet 7 weniger als dreimal mehr….
Max bezahlt mit seinem Handy-Abo 15 Rappen pro SMS. Roger bezahlt nur 5 Rappen pro SMS, dafür eine monatliche Grundgebühr für die SMS-Option von 3 Franken. Ab wie vielen SMS lohnt sich die SMS-Option für Roger?
Lösung:
Max: 15 Rappen pro SMS
Roger: 5 Rappen pro SMS plus monatliche Grundgebühr von 3 Franken.
0.15 * x = 0.05 * x + 3
0.15x – 0.05x = 3
0.1x = 3
x = 30
Max im Monat:
30*0.05 + 3 = 4.50
Roger im Monat:
30*0.15 = 4.50
Ab 30 SMS lohnt sich die Option.